Вычислить объем тела, образуемого вращением вокруг оси ОХ трапеции, ограниченной линиями
у=0, х=0, х=6.
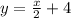
Другие вопросы по теме Математика
Популярные вопросы
- Почему саныч боялся предательств из облачного полка ?...
3 - Краткий рассказ о политике и франции в 19 веке надо...
3 - Термин зародился в среде древнегреческих стоиков.древнеримский грамматист варрон...
1 - Звуко-буквений аналіз слова ряску...
2 - Какая страна всегда стояла на защите италии? ...
2 - Классифицировать по конституции рф права человека и гражданина на личные, политические...
2 - Длина комнаты 400 см, ширина – 3 м. какова площадь комнаты в квадратных метрах?...
3 - Язык8 класскак девушка впечатлительная, она быстро проникалась новыми ощущениями,...
1 - Назовите понятие, общее для ниже, объединяющее их: семья, государство, производство,...
1 - Кого из писателей 18 века бросила жена? ...
3
Шаг 1: Найдите функцию, определяющую верхнюю границу трапеции. В данном случае, нам дано уравнение прямой y = (1/2)x + 4.
Шаг 2: Найдите точки пересечения трапеции с осями. В данном случае, трапеция пересекает ось OX в точках (0,0) и (6,0).
Шаг 3: Найдите интеграл функции (1/2)x + 4, взятый между x=0 и x=6. Интеграл функции позволяет нам найти площадь поверхности вращения трапеции вокруг оси OX.
Интеграл функции (1/2)x + 4 можно вычислить следующим образом:
∫[(1/2)x + 4] dx
= (1/4)x^2 + 4x + C
где С - постоянная интегрирования.
Шаг 4: Подставьте значения верхней и нижней границы интеграла.
При подстановке верхней границы x=6 получим:
(1/4)(6^2) + 4(6) + C
= (1/4)(36) + 24 + C
= 9 + 24 + C
= 33 + C
При подстановке нижней границы x=0 получим:
(1/4)(0^2) + 4(0) + C
= 0 + 0 + C
= C
Шаг 5: Найдите разность значений функции интеграла (∫[(1/2)x + 4] dx) при верхней и нижней границах.
Таким образом, объем тела, образованного вращением трапеции вокруг оси OX, можно найти как разность площадей поверхностей, полученных при вращении функции (1/2)x + 4 от x=0 до x=6:
V = 33 + C - C = 33.
Ответ: Объем тела, образованного вращением трапеции вокруг оси OX, равен 33 кубическим единицам.