1. Математика
  2. Вычислить несобственные

Вычислить несобственные интегралы или установить их расходимость.
Можно выполнить на листе бумаги и прикрепить фото.

mam40 mam40    1   19.05.2020 12:20    0

Ответы
NurGangsta NurGangsta  15.10.2020 00:13

Имеем несобственный интеграл 1-го рода:

\int^{\infty}_2\frac{dx}{4+x^2}

По формуле: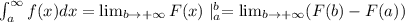 \int^{\infty}_af(x)dx= \lim_{b \to +\infty} F(x)\mid^b_a= \lim_{b \to +\infty}(F(b)-F(a)) имеем:

\int\frac{1}{4+x^2}dx=\frac{arctg(\frac{x}{2}) }{2}+C\\\\ \lim_{b \to +\infty} \frac{arctg(\frac{x}{2}) }{2}\mid^b_2= \lim_{b \to +\infty} (\frac{arctg(\frac{b}{2}) }{2}-\frac{arctg(\frac{2}{2}) }{2})= \lim_{b \to +\infty} (\frac{arctg(\frac{b}{2}) }{2}-\frac{\frac{\pi}{4} }{2})=\\\\ =\frac{\pi}{4}-\frac{\pi}{8}=\frac{\pi}{8}

Как видно из результата - интеграл сходится.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Sanyaaa12 Sanyaaa12  23.12.2019 19:11
Ккаким сферам жизни общества относят следующие элементы: а)промышленное и сельскохозяйственное производствоб) учрежденияв)политика, право, государство,политические партииг)наука,...
nector nector  23.12.2019 19:11
Срешением. отмечу как лучший ответ ​...
Глобабутаканкулятор Глобабутаканкулятор  23.12.2019 19:11
Можете начертить небольшую схемку по этой ! мотоциклист догоняет велосипедиста.сейчас межлу ними 23,4 км.скорость велосипедиста 13,2 км. найдите скорость мотоциклиста,если...
kostyatar2016 kostyatar2016  23.12.2019 19:11
Визначи площу зафарбованої фігури, якщо радіус круга дорівнює 1,8 см, а довжина сторони квадрата - 1,2 см....
Leo100Danik1 Leo100Danik1  23.12.2019 19:11
Розв яжіть рівняння я вообще не понимаю пытался розобратся и спрашивал у родителей никто не помнит как решить ​...
Horse3333 Horse3333  23.12.2019 19:10
Раскройте скобки и подобные слагаемые : 0,2(3х - 3,5) - 5(4,8 - х) + 0,7​...
Xaler Xaler  23.12.2019 19:09
Вычислите используя распределительное свойство умножения относительно сложения : (-3,6 : 0,4 * (-0,2)) : (-0,3 - 1,5 - 0,7 * 1,5)​...
FruitAPps FruitAPps  23.12.2019 19:09
Разделите длинной записью ! 6048: 112 6048: 504 6048: 432...
Mамикс Mамикс  23.12.2019 19:09
(2,5*10^8)(3*10^-10) и 0,08 сравнить, последние , надежда на вас....
Frisk011 Frisk011  23.12.2019 19:09
Пятеро каменщиков вначале рабочей недели получили равное количество кирпича. когда трое из них израсходовали по 326 кирпичей, то у них осталось столько кирпичей, сколько вначале...

Популярные вопросы