Вычислить неопределенный интеграл
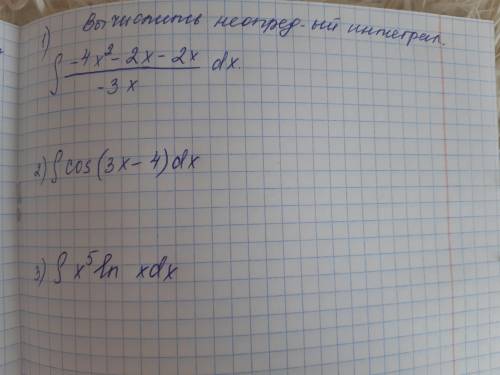
Другие вопросы по теме Математика
Популярные вопросы
- 2. Периметр треугольника ABC 88 см. Сторона АВ 3 раза больше...
2 - Запиши 5 вопросов к рассказу праздник весны ответь на них...
1 - 1. Написать ( НЕ меныше трёх) уравнения химических реакций в...
2 - Назовите единицу работы в CI и дайте её значение...
3 - Мы смотрели телевизор вчера он ходил в парк вчерая купил сыр...
3 - буду очень благодарен. Заранее...
3 - Образ главной героини в поэме Руслан и Людмила дать описание,...
2 - Які рослини і тварини поширені в херсонській області? Як вони...
3 - Расставьте пропущенные знаки препинания. Объясните их постановку...
2 - Стр. 53 читать, переводить, подобрать подходящий заголовок,...
3
1.
2.
3.
По частям: