Вычислить интеграл } \, dx)
Другие вопросы по теме Математика
Популярные вопросы
- Обозначить пунктограммы над рекою пухлыми клочьями проворно...
2 - 4градуса северной широты и 10 градусов восточной долготы...
1 - 1)дайте характеристику эраста из повести бедная лиза по плану:...
1 - Микола вже був немолодий хлопець, а чоловік з довгими вусами,...
3 - Help поже отличия летописи от песни до завтра надо...
3 - Thursday morning classes nora was the street....
3 - Придумай рассказ и запиши его в творческую тетрадь...
2 - Назовите 10 трубчатых грибов и 10 пластинчатых назовите их сходства...
3 - Впервом спичечном коробке было в 3 раза больше спичек чем во...
2 - Решить закончить за 1 3/4 часа потратили на 2/5 часа чем закончили...
3
ответ: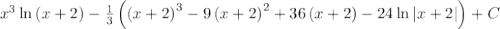
Пошаговое объяснение: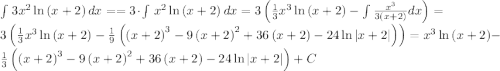
Пошаговое объяснение: