Вычислить интеграл e^3x cos^2 * x dx распишите поподробнее, если возможно.
Ответы
Вот как вижу так и решаю.
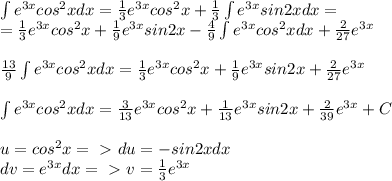
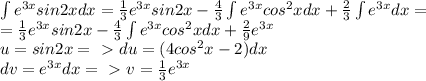
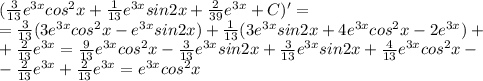
ПОКАЗАТЬ ОТВЕТЫ
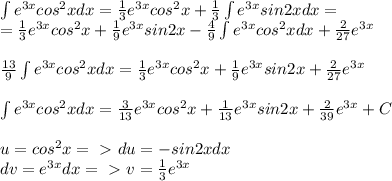
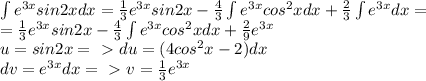
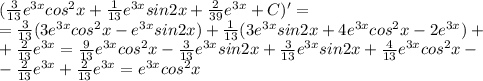
Другие вопросы по теме Математика
Популярные вопросы
- Согласный,образуемый при одного шума,без участия голоса...
2 - Ебаратынский югом дохнула зима отдыхает найти стих...
3 - Окр.мир 4кл.-творческая работа-сформируй свои собственные питания и обьясни...
3 - Он в слове мать ,и в слове дочь, и в тихом лунном слове ночь, чтоб никого...
2 - Корень 3 степени из а умножить на корень 3 степени из а...
1 - Решите пропорции: х/9=5/7 5/х=0,2/3 6х/5=18/7...
2 - 12-(x+3 4 и 5 дробные)=2 1 и 5 дробные...
3 - Что такое обоснование проекта и как его можно разложить...
1 - Как отрицательно ответить на вопрос - is your birthday in august?...
1 - 50 нужно написать текст-рассуждение (небольшой) на тему: есть люди настолько...
2