Вычислить интеграл (4x-2x^2) ln x dx
Другие вопросы по теме Математика
Популярные вопросы
- Сколько коробок понадобится,чтобы разложить 18 карандашей так,чтобы...
3 - Сочинение на тему почему надо заниматься спортом 15 предложений...
2 - Нужна письменый отзыв о тарасе бульбы о его сыновьях о произведение...
2 - Мне нужно найти сходство и различие между казахским народом и кыргызским...
1 - Как автор в своём рассказе муму раскрывает проблему крепостничества...
2 - Сөйлемді толықтырып жаз. 1. 2. і 3. ңдады 4. і 5. 6. қарады 7. і...
1 - Вabc ab=ac. высота bm равна 9 см и делит боковую сторону ac на два...
3 - Сочинение на тему международное положение руси в 10-15 веках....
3 - ответить на зачу вот : мама заготовила 6 трёхлитровых баннок яблочного...
3 - Напишите сочинение на тему россия можно использовать и композиторов...
3
Пошаговое объяснение:
{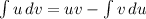 ; для первого интеграла u=lnx du=
; для первого интеграла u=lnx du=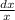 dv=xdx v=
dv=xdx v=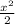
для второго интеграла u=lnx du=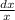 dv=
dv=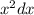 v=x³/3}
v=x³/3}
=4(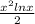 -
-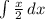 ) - 2((x³lnx)/3-
) - 2((x³lnx)/3-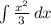 )=2x²lnx-x²-
)=2x²lnx-x²-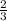 x³lnx+
x³lnx+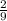 x³+C
x³+C