вычислить границу функции.
Другие вопросы по теме Математика
Популярные вопросы
- Спишите, вставляя пропущенные буквы, расставляя недостающие знаки...
1 - Предложения про заповедник ...
1 - Abc c=90⁰ AC=10⁰ A=45 AB?...
3 - Визначте вид відокремленого члена речення. Сікач, незважаючи на...
3 - обчисліть і вкажіть масовуу частку розчиненої речовини в розчині...
1 - ДУЖЕ Установіть відповідність між рекреаційними ресурсами та їхньою...
1 - Отметьте только те слова или сочетания слов, которые выступают...
3 - Укажіть продукцію, великим експортером якої є Бразилія. а) сірчана...
3 - Дано трикутник A B C. побудувати бісектрису кут C до A B...
3 - Нужно написать БОЛЬШОЕ эссе по философии на тему «Без цели нет...
3
Для нахождения пределов такого вида воспользуйтесь теоремой о втором замечательном пределе: имеет место соотношение вида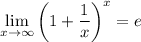 или
или 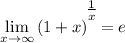 .
.