Вычислить длину дуги кривой y= корень 5x^3 в пределах x=0 до x=1
Ответы
Длина кривой вычисляется по 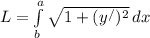
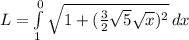 =...=
=...=
ПОКАЗАТЬ ОТВЕТЫ
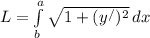
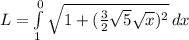 =...=
=...=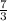
Другие вопросы по теме Математика
Популярные вопросы
- Из точки А,лежащей вне плоскости а,проведены на плоскость перпендикуляр АВ...
1 - 271. С графикафункции f(x) на рис. 59 укажитепромежутки возрастания, убы -вания...
3 - Раскрыть скобки и привести подобные слагаемые: 4 (3х - 7) – (12 + 11х)....
1 - Шуліка помітивши на землі здобич, стрімголов кидається у них.У момент пікірування...
3 - Про дівчинку, яка пішла шукати воду для хворої матері, йдеться у твор Про Зоряний...
3 - От Необходимо глагол finden...
3 - Мд =17см мс=10 см найдите аб ...
2 - Перевести у системні одиниці:5см;3мм;6кДж;12МН;4мк Па...
3 - Силіцій масою 420 г спалили в атмосфері кисню. У результаті реакції утворилося...
3 - До ть будь ласка!До 950 г води додали 50 мл 48 - відсоткового розчину сульфатної...
2