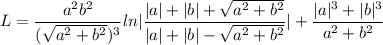Вычислить длину дуги кривой при интеграла

Другие вопросы по теме Математика
Популярные вопросы
- Какой подход для определения количества информации был использован...
1 - Які фізичні та хімічні явища утворення розчину?...
2 - Выпишите пять слов с проверяемыми безударными гласными.подберите...
2 - Сделай морфологический разбор имён прилагательных. над зеленом...
3 - Значение выражения a+2-13 равно нулю, если a=...
1 - Какие параметры системы надо поддерживать постоянными, чтобы по...
3 - Производная функции y=cosx-3x² в точке x0=0 равна ? , ....
3 - Доведіть, що коли прямі ас і вd мимобіжні, то прямі ав і сd теж...
1 - Ch3 ch3-ch-ch-ch3 h3c-ch2 скажите название...
3 - Придумать 5 предложения слово общественный транспорт ...
1
Пусть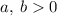 Тогда
Тогда 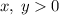 . Также, т.к. корень - число неотрицательное, то
. Также, т.к. корень - число неотрицательное, то 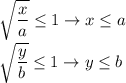 .
.
Теперь заменим на противоположное число
на противоположное число 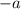 . Заметим, что теперь
. Заметим, что теперь 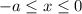 и каждому значению функции, соответствующее каждому значению аргумента, соответствует противоположный аргумент. Проведя аналогичные действия для
и каждому значению функции, соответствующее каждому значению аргумента, соответствует противоположный аргумент. Проведя аналогичные действия для 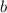 , заметим, что изменение знака параметров на противоположные лишь отображает график относительно координатных осей, но не меняют длину кривой. Тогда достаточно найти длину кривой для положительных
, заметим, что изменение знака параметров на противоположные лишь отображает график относительно координатных осей, но не меняют длину кривой. Тогда достаточно найти длину кривой для положительных 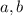 , а затем в получившейся формуле заменить
, а затем в получившейся формуле заменить  на
на 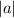 ,
, 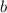 на
на 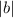 .
.
Теперь запишем параметрическое задание функции.
Пусть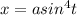 . Тогда
. Тогда 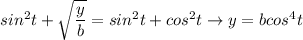 ,
, ![t\in[0;\dfrac{\pi}{2}]](/tpl/images/0672/7264/77f83.png) .
.
Вычисление длины кривой на фото 1 и 2. На 3 фото вычисление вс интеграла.
Теперь остается лишь подставить модули параметров. Получаем