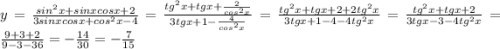Вычислить: 1) y=(3sin^2(x)+2cos^2(x)-1)/(sin^2(x)-sinx*cosx+2) если tgx=1 2) y=(sin^2(x)+sinx*cosx+2)/(3sinx*cosx+cos^2(x)-4) если tgx=3
Другие вопросы по теме Математика
Популярные вопросы
- Вставь пропущенные единицы массы и запиши верные равенство.1)=...
1 - Любое число содержащее 134 единицы i класса и 75 единиц ii класса.!...
2 - Словосочетание место.+ сущ, с всякий?...
2 - Как разобрать прилагательное как часть речи, прилагательное: потоплённые,...
1 - Как выполнить прикидку деления: 1624272: 312...
3 - Есть 3 шкатулки.в них лежат по 2 драгоценных камня. в одной -2...
1 - Появление синего окрашивания при взаимодействии йодной настойки...
2 - Почему в слове дождливый не пишется мягкий знак ?...
3 - Написати п ять речень з однорідними членами, вираженими прислівниками....
1 - 10 речень з відокремленою обставиною...
2
Відповідь:
Числитель и знаменатель первой дроби ( в 1 и 2 задании) делим на cos^2(x).
Покрокове пояснення:
1)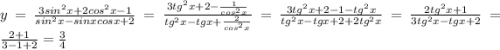
2)