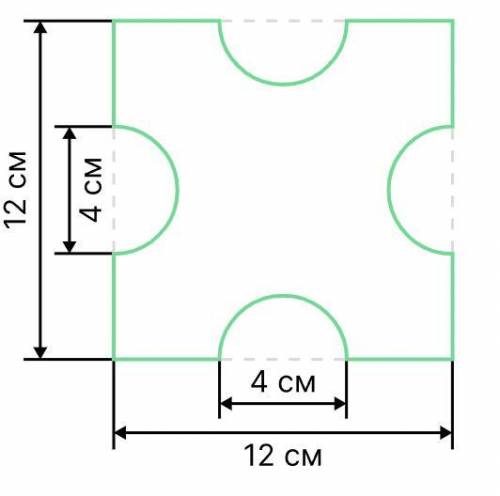
Вычисли длину зелёной линии.

Для вычисления длины зелёной линии, нам понадобятся некоторые геометрические знания о треугольниках и кругах. Давайте рассмотрим данную фигуру и построим несколько вспомогательных линий.

Первым шагом мы можем построить перпендикуляр из середины основания треугольника к его основанию. Этот перпендикуляр разделит основание на две равные части и пересечется с вершиной треугольника. Давайте обозначим точку пересечения этого перпендикуляра с вершиной как точку А.

Теперь, давайте построим прямую линию от вершины треугольника А через его центр (середину основания) и до точки на границе круга. Обозначим эту точку пересечения как точку В.

Мы можем заметить, что это новая прямая линия создает прямоугольный треугольник, где линия, от точки В до центра круга, является радиусом круга, и линия от точки А до центра круга, является еще одним радиусом круга.

Теперь, чтобы вычислить длину зеленой линии, нам нужно вычислить длину части зеленой линии от точки А до точки В и удвоить эту длину.

Для вычисления этой части зеленой линии, мы можем заметить, что она состоит из двух радиусов круга и одной стороны прямоугольного треугольника. Таким образом, длина этой части зеленой линии может быть рассчитана следующим образом:

Длина зеленой линии = 2 * (Радиус + Радиус + Сторона прямоугольного треугольника)

Теперь нам осталось только вычислить радиус и сторону прямоугольного треугольника.

Радиус:
Для нахождения радиуса круга, нам нужно найти половину длины основания треугольника. Мы можем использовать середину основания треугольника, которая является концом перпендикуляра, построенного из середины основания. Таким образом, чтобы получить радиус, мы должны разделить длину основания треугольника на 2.

Радиус = Длина основания / 2

Сторона прямоугольного треугольника:
Для нахождения стороны прямоугольного треугольника, мы можем использовать теорему Пифагора, так как эта сторона является гипотенузой треугольника.

Теорема Пифагора гласит: a^2 + b^2 = c^2, где c - гипотенуза, а a и b - катеты.

В данном случае, катеты равны половине длины основания и радиусу, а гипотенуза равна стороне прямоугольного треугольника. Таким образом, мы можем использовать следующую формулу для вычисления стороны прямоугольного треугольника:

Сторона прямоугольного треугольника = sqrt((Радиус^2) + (Половина длины основания)^2)

После того, как мы найдем радиус и сторону прямоугольного треугольника, мы можем заменить эти значения в нашу исходную формулу для длины зеленой линии и вычислить ответ.

Пожалуйста, используйте данные из наглядности (длину основы и радиус), чтобы рассчитать ответ на этом этапе. Если вам нужна помощь в решении данного вопроса, пожалуйста, предоставьте эти значения, чтобы я мог продолжить решать задачу.