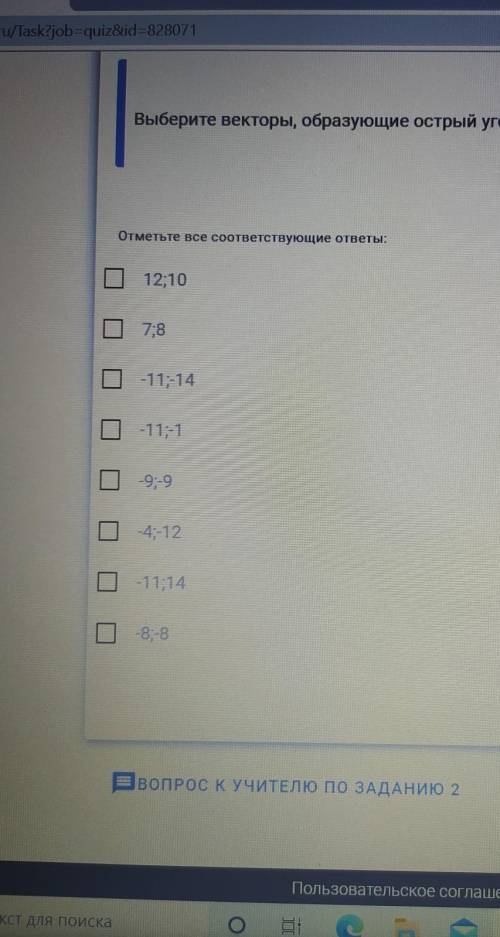
Выберите векторы, образующие острый угол с вектором
→ a { −8; 11}.​

Чтобы найти векторы, образующие острый угол с вектором a {-8; 11}, нужно использовать определение скалярного произведения векторов.

Скалярное произведение векторов можно найти по формуле: a · b = |a| |b| cos α, где a и b - векторы, α - угол между ними.

Так как нам нужны векторы, образующие острый угол с вектором a, то мы можем заменить угол α на угол между векторами и использовать формулу a · b = |a| |b| cos β.

Для каждого вектора на рисунке, мы должны найти его координаты и выразить его в виде вектора с началом в начале координат.

Давайте рассмотрим вектор А (3; 4):
A = {3; 4}

Теперь рассмотрим вектор B (2; -5):
B = {2; -5}

Теперь нам нужно найти скалярное произведение вектора a {-8; 11} с вектором A и B.

Для вектора A:
(a · A) = (-8 * 3) + (11 * 4) = -24 + 44= 20

Для вектора B:
(a · B) = (-8 * 2) + (11 * -5) = -16 - 55 = -71

Теперь, когда у нас есть скалярное произведение каждого вектора с вектором a, мы можем применить определение скалярного произведения: a · b = |a| |b| cos β.

Так как sin острого угла между вектором a и вектором равен положительному числу, cos β должен быть положительным.

В нашем случае, a · A = 20 и a · B = -71.

По определению скалярного произведения, a · A > 0 и a · B < 0, это означает, что вектор A образует острый угол с вектором a, а вектор B образует тупой угол (или острый угол между π/2 и π).

Таким образом, вектор A {3; 4} образует острый угол с вектором a {-8; 11}.