Выберите пары элементов множества А={12; 16; 28; 32; 40; 45, 56}, отношения которых равны {3/4;1/2;4/5;5/7;2/5;3;10} Нужно подробное решение

Пошаговое объяснение:

Нужно составить всевозможные пары (числитель–знаменатель), состоящие из элементов множества, где первое число меньше второго (все данные отношения меньше 1), всего 21 вариант. После сокращения каждой из дробей сравнить с приведенными отношениями, выбрать правильные соотношения.

1) С числителем 12: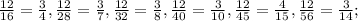

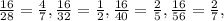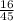2) С числителем 16: дробь несократима;

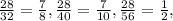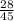3) С числителем 28: дробь несократима;

4) С числителем 32: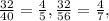 дробь 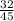несократима;

5) С числителем 40: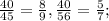

6) С числителем 45: дробь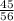 несократима.

Таким образом, отношение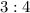 дают пара 12–16; 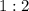— пары 16–32 и 28–56; 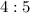— пара 32–40; 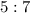— пара 40–56; 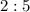— пара 16–40; 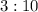— пара 12–40.