Выберите функции, которые являются показательными
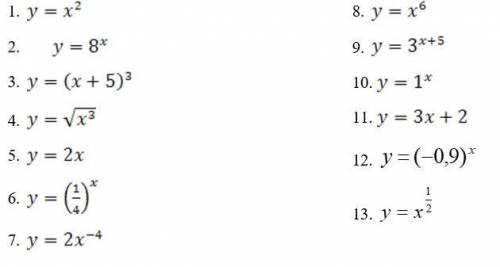
Другие вопросы по теме Математика
Популярные вопросы
- Fill in the gaps with the words and expressions : ingenious, in vitro...
3 - Imagine a relative in america gave you an experience gift for your...
3 - Нетрадиционные получения электроэнергии...
2 - Дай полный ответ на вопрос: бог анубис имел тело человека и голову...
3 - На доске написано пять последовательных натуральных чисел. когда...
1 - Вычислите массу хлорида натрия необходимого для приготовления 240г...
2 - 2: 2. подберите различные антонимы (слова с противоположным значением)...
1 - Write down the words with these sounds: {ei} {ju: } {x} {i} {eə}...
3 - Укажите вид предложения по количеству грамматических основ. все называли...
3 - Мат.анализ. доказть для любого натурального числа уравнение 5*2^3n-2+3^3n-1...
3
Показательная функция - это функция, в которой независимая переменная (обычно обозначается как x) является показателем, возводящим основание (обычно обозначается как a) в степень.
На картинке даны четыре возможных функции, и нам необходимо определить, какая из них является показательной.
1. Функция A(x) = x2 - это квадратная функция. Она не является показательной, потому что показатель (2) не включает переменную x. Таким образом, функция A(x) НЕ является показательной.
2. Функция B(x) = 5x - это показательная функция, потому что независимая переменная x является показателем, возводящим основание 5 в степень. Ответ: функция B(x) ЯВЛЯЕТСЯ показательной.
3. Функция C(x) = 3x + 2 - это линейная функция. Она не является показательной, потому что в ней отсутствует возведение основания в степень. Таким образом, функция C(x) НЕ является показательной.
4. Функция D(x) = log4(x) - это логарифмическая функция. Она не является показательной, потому что в ней используется логарифмическая операция, а не возведение в степень. Таким образом, функция D(x) НЕ является показательной.
Итак, из четырех предоставленных функций только функция B(x) = 5x является показательной.