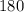Ввозрастающей прогрессии b1+b2+b3=215. числа b1+12; b2+25; b3-87 составляют арифметическую прогрессию. найдите b3
Другие вопросы по теме Математика
Популярные вопросы
- хорда ab пересекает диаметр окружности в точке m и его в отношении...
1 - Қазақстанның жан-жануарлар әлемі Диалогті оқы, ішінен оған тақырып...
3 - ТЕМ КТО ОТВЕТИТ А НЕ ТЕМ КТО ПРОСТО НАПИШЕТ ЕРУНДУ...
3 - Определите эру с самой большей продолжительностью?...
1 - Либералды идеялардың негізі қағидасын атай аласың ба...
2 - 1. Луч падает на зеркало по углом 30°. На какой угол отклонится...
3 - | Ралым Ахмедов) 1. Ақсақ Темір деген кім? Ол туралы не білесіңдер?2....
2 - 5 Study the examples with by and on in exercise 4. Ask and answer...
2 - Жетінші сөзіне сөйлем құрау...
2 - Информация про Машук.Как она погибла? как она попала на войну? какой...
3
Воспользуемся формулой n-го члена геометрической прогрессии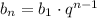 и перепишем равенство следующим образом:
и перепишем равенство следующим образом:
Тогда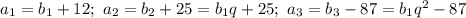 образуют арифметическую прогрессию. Воспользуемся характеристическим свойством арифметической прогрессии, а именно
образуют арифметическую прогрессию. Воспользуемся характеристическим свойством арифметической прогрессии, а именно 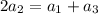 . Таким образом,
. Таким образом,
Получили систему уравнений с двумя переменными:
Поделим почленно оба уравнения:
Следовательно,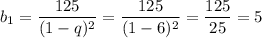
Значит,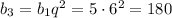
ответ: