Вурне а черных и (а+1) белых шаров. случайным образом вынимают (а+1) шаров. найти вероятность того что среди них окажется: а) а белых шаров б)не более чем а белых шаров (а=4)

Перепишу условие, подставив а = 4.

В урне 4 черных и 5 белых шаров. Случайным образом вынимают 5 шаров.  Найти вероятность того что среди них окажется:

а) 4 белых шаров;

б) не более чем 4 белых шаров.

Общее число возможных элементарных исходов для данных испытаний равно числу которыми можно выбрать 5 шаров из 9:

Пусть случайная величина Х — появление белого шара;

Подсчитаем число исходов, благоприятствующих данному событию:

a) Выбрать четыре белых шаров можно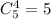 а один черный шар — 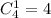По правилу произведения, всего таких

Искомая вероятность: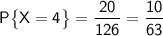

б) Здесь нужно посчитать вероятность через противоположное событие, то есть: