Втреугольнике авс со сторонами ав=вс=15 и ас=18 найдите расстояние от вершины в до точек пересечения а) медиан , б) биссектрис, в) серединных перпендикуляров сторон ,г) высот

Ответы

Lalker1337 04.10.2020 01:31

Так как каждый пункт рассматривается в качестве отдельной задачи, замечательные точки треугольника всегда будут называться O.

а) BM₂ точкой пересечения медиан делится в отношении BO : OM₂ = 2 : 1 ⇒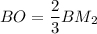 $BO=\dfrac{2}{3}BM_2$ .

Так как AB = BC, BM₂ — высота. По теореме Пифагора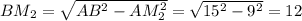 $BM_2=\sqrt{AB^2-AM_2^2}=\sqrt{15^2-9^2}=12$ .

Тогда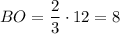 $BO=\dfrac{2}{3}\cdot 12=8$

б) Точка пересечения биссектрис — центр вписанной окружности. Так как AB = BC, BB₂ — высота ⇒ OB₂ — радиус (r) вписанной окружности.

Площадь треугольника ABC

$S_{ABC}=\dfrac{1}{2}\cdot BB_2\cdot AC=\dfrac{AB+BC+AC}{2}\cdot r\Rightarrowr=\dfrac{BB_2\cdot AC}{AB+BC+AC}=\\=\dfrac{12\cdot 18}{15+15+18}=4{,}5\Rightarrow BO=BB_2-OB_2=12-4{,}5=7{,}5$

в) Точка пересечения серединных перпендикуляров — центр описанной окружности ⇒ OB — радиус (R) описанной окружности. Площадь треугольника ABC

$S_{ABC}=\dfrac{1}{2}\cdot AC\cdot BH_2=\dfrac{AB\cdot BC\cdot AC}{4R}\Rightarrow R=\dfrac{AB\cdot BC}{2BH_2}=\dfrac{15^2}{2\cdot 12}=9{,}375$

г) Площадь треугольника ABC

$S_{ABC}=\dfrac{1}{2}\cdot AC\cdot BH_2=\dfrac{1}{2}\cdot BC\cdot AH_1\Leftrightarrow AH_1=\dfrac{AC\cdot BH_2}{BC}=\dfrac{18\cdot 12}{15}=\dfrac{72}{5}\\\cos{\angle{CAH_1}}=\dfrac{AH_1}{AC}=\dfrac{72}{5\cdot 18}=\dfrac{4}{5}\Rightarrow \sin{\angle{CAH_1}}=\dfrac{3}{5}\Rightarrow tg~\angle{CAH_1}=\\=\dfrac{\sin{\angle{CAH_1}}}{\cos{\angle{CAH_1}}}=\dfrac{3}{4}=\dfrac{OH_2}{AH_2}=\dfrac{OH_2}{9}\Rightarrow OH_2=\dfrac{9\cdot 3}{4}=6{,}75\Rightarrow BO=BH_2-\\-OH_2=12-6{,}75=5{,}25$