Втреугольник abc вписан прямоугольник так, что две его вершины лежат на стороне ac, а две другие - на сторонах ab и вс. найдите наибольшее значение площади такого прямоугольника, если ас=12 см, вд=10см, где bd - высота треугольника abc. , ,
Другие вопросы по теме Математика
Популярные вопросы
- Проанализировав текст, соотнеси данные. Согласно переписи населения...
3 - 1 326. Из двух городов навстречу друг другу одновременно вышли два...
3 - Сумма углов треугольника. Внешний угол треугольника. Урок 5 AB ∦...
2 - Какая роль животных в медицине...
1 - 8. Ветань пропущенные буквы. Укажи спря- жение глаголов с пропущенными...
2 - Почему Тургенев назвал рассказ Муму. Развёрнутый ответ. Примерно...
3 - Найдите уравнение касательной для x0=4 объясните максимально подробно...
3 - Решить неравенствох²-15х+26 =0...
2 - Здравствуйте нарисуйте и напишите слова...
2 - 4. Проба пераЗаполни таблицу. Сравни чувства, поведение героев в...
2
Отметим точки E и F прямоугольника EGHF на стороне AC, а точку G и H на сторонах AB и BC соответственно. Пересечение высоты BD и отрезка GH отметим через D1.
Обозначим GH через x.
Т.к. в прямоугольнике EGHF сторона GH параллельна стороне EF, которая лежит на стороне AC треугольника ABC, то GH || AC, а следовательно ΔGBH≈ΔABC
Тогда
Отметим, что GE = DD1 и найдем площадь прямоугольника EGHF:
Т.е. нам надо найти максимум функции
Для этого найдем ее производную и приравняем 0:
Значит x = 6 является точкой максимума функции.
Значение функции в точке максимума: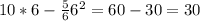
ответ: наибольшее значение площади такого прямоугольника 30 см2