Впервом ящике 1 белый, 2 красных и 3 синих шара;
во втором ящике 2 белых. 6 красных, 4 синих шара. из каждого
ящика вынули по шару. какова вероятность, что среди вынутых
шаров нет синих?

Ответы

nataliolejic 17.08.2020 15:48

Вероятность достать белый шар из первого ящика равна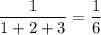 $\dfrac{1}{1+2+3}=\dfrac{1}{6}$ , а вероятность достать белый шар из второго ящика равна 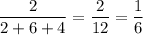$\dfrac{2}{2+6+4}=\dfrac{2}{12}=\dfrac{1}{6}$ . По теореме умножения, вероятность того что среди вынутых шаров оба окажутся белыми равна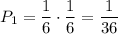 $P_1=\dfrac{1}{6}\cdot\dfrac{1}{6}=\dfrac{1}{36}$

Вероятность достать красный шар из первого ящика равна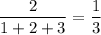 $\dfrac{2}{1+2+3}=\dfrac{1}{3}$ , а вероятность достать белый шар из второго ящика равна 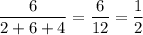$\dfrac{6}{2+6+4}=\dfrac{6}{12}=\dfrac{1}{2}$ . По теореме умножения, вероятность того что среди вынутых шаров оба окажутся красными равна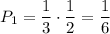 $P_1=\dfrac{1}{3}\cdot\dfrac{1}{2}=\dfrac{1}{6}$

Вероятность достать белый шар из первого ящика равна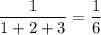 $\dfrac{1}{1+2+3}=\dfrac{1}{6}$ , а вероятность достать красный шар из второго ящика равна 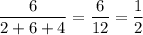$\dfrac{6}{2+6+4}=\dfrac{6}{12}=\dfrac{1}{2}$ . По теореме умножения, вероятность того что среди вынутых шаров из первого ящика окажется белый шар, а из второго - красный равна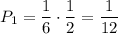 $P_1=\dfrac{1}{6}\cdot\dfrac{1}{2}=\dfrac{1}{12}$

Вероятность достать красный шар из первого ящика равна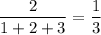 $\dfrac{2}{1+2+3}=\dfrac{1}{3}$ , а вероятность достать белый шар из второго ящика равна 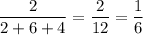$\dfrac{2}{2+6+4}=\dfrac{2}{12}=\dfrac{1}{6}$ . По теореме умножения, вероятность того что среди вынутых шаров из первого ящика окажется красный шар, а из второго - белый равна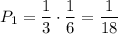 $P_1=\dfrac{1}{3}\cdot\dfrac{1}{6}=\dfrac{1}{18}$

По теореме сложения, вероятность того, что среди вынутых шаров нет синих равна

$P=\dfrac{1}{36}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{18}=\dfrac{1}{3}$

ответ: 1/3.

ПОКАЗАТЬ ОТВЕТЫ

nastea030 17.08.2020 15:48

Из первого несиний шар можно вынуть с вероятностью3/6.из второго - не синий с вероятностью 8/12.Вероятность того, что из обоих ящиков вынут не синий шар равна произведению этих вероятностей, то есть

3/6 * 8/12 =1/2 * 2/3 =1/3.

вероятность того, что среди вынутых шаров нет синих равна 1/3

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика