Впервом сосуде содержится 50 кг а во втором 30 кг раствора кислоты различной концентрации. если эти растворы смешать то получится раствор содержащий 55% кислоты. если же смешать равные массы этих растворов то получится раствор содержащий 60% кислоты. сколько кг кислоты содержится в первом сосуде.

Пошаговое объяснение:

х-концентрация первого раствора (в долях от 1)

у - второго

тогда масса кислоты в 1 растворе 50х

масса кислоты во втором растворе 30у

(присмешивании будет 80 г 55% раствора)

50х+30у=44 - первое уравнение

если смешать равные массы (пусть по 30г), тогда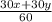 =0,6

30х+30у=36

получилась система уравнений

выразим у из второго

30у=36-30х

у=1,2-х

подставим в 1 уравнение

50х+30(1,2-х)=44

50х+36-30х=44

20х=8

х=0,4

50*0,4=20кг кислоты в первом растворе

Пошаговое объяснение:

Пусть x% - концентрация раствора в первом сосуде, а y% - концентрация раствора во втором сосуде. Так как первый сосуд содержит 50 кг, а второй — 30 кг растворов кислоты, то суммарная масса кислоты в обоих сосудах, равна   50х+30у  

. В задаче указано, что если растворы смешать, то получится раствор, содержащий 55% кислоты, то есть массу кислоты в них можно выразить  0,55(50+30)=0,55*80 .

Получаем уравнение:

50х+30у=0,55*80

50х+30у= 44

Второе уравнение получается из второго условия: если смешать равные массы этих растворов 1*х+1*у , то получится раствор, содержащий 60 % кислоты 0,6(1+1)=0,6*2 . Имеем уравнение:

х+у=0,6*2

х+у=1,2

Получаем систему уравнений:

50х+30у=44

х+у=1,2

умножим второе уравнение на -30

-30х-30у=-36

И схожим с первым уравнением

20х=8

х=8:20

х=0,4

то есть имеем в первом сосуде раствор 40% концентрации

значит масса кислоты будет

0,4*50= 20 кг