Вот еще, можно так подробно не расписывать, но реши хоть что-нибудь из этого, , если сможешь решить несколько буду : )
область определения функции:
1) y=(1/2)^1/х + arcsin((x+2)/3)
2) y= e^корень из x * log2(2-3x)
3) y= arccos(x-2)-ln(x-2)
Другие вопросы по теме Математика
Популярные вопросы
- Решить, . решается как-то в пи. 2arccos1+3arccos0 5cos(arccos1/3)-2cos(arccos1/4)...
2 - Понимаю лета, но ! обеспечено! а3. в равнобедренном треугольнике боковая...
1 - Чему равна площадь параллелепипеда?...
2 - Расставить коэффициенты в уравнении: zn+hno3=zn(no3)2+no2+h2o...
3 - Докажите теоретически, что для спиртов характерны реакции частичного и...
3 - Отношение 4/9 : 1 1/5 .интересует решение....
1 - Дано вершини a(2; 1) b(3; 2) с(5; 2) трикутника авс.знайти рівняння і довжину...
1 - Вчем измеряется формула тонкой линзы...
1 - 1) уравнение движения: s=t^2-3t. найти мгновенную скорость движения за...
3 - Какая главная мысль произведения “илья муромец и соловей -разбойник ”...
2
1) D(f)∈[-5;0)∪(0;1]
2) D(f)∈[0;2/3)
3) D(f)∈(2;3]
Пошаговое объяснение:
y=(1/2)^1/х + arcsin((x+2)/3)
Рассматриваем данную функцию по частям:
1) y=(1/2)^1/х
В степени стоит выражение 1/x и оно похоже на функцию,график которой и есть та самая гипербола!
Вспомним,что x≠0 или иначе на ноль делить нельзя! Поэтому точка 0 есть как первая критическая точка.
Поэтому обл. определения функции y=(1/2)^1/х является D(f)∈ (-∞;0)∪(0;+∞)
2) y=arcsin((x+2)/3)
В функции есть обратная тригон. функция y=arcsin (x).
Вспомним,что область определения такой функции является:
D(f)∈(-1;1)
Поэтому функция y=arcsin((x+2)/3) будет смещена,а поэтому область определения будет смещена.
Запишем такой неравенство используя область определения y=arcsin (x): D(f)∈(-1;1) :
-1≤x+2/3≤1
Решаем неравенство через систему:
И получаем
x≤1 ; x≥-5
Тогда D(f)∈[-5;1]
В итоге построим ось x объединяя все наши расчеты:
---------*-5----------------°0------------------*1------->x
И у нас получается:
-5≤0≤1
Запишем в область определения D(f)∈[-5;0)∪(0;1]
Где * и ° - невыколотая и выколотая точка
y= e^√x * log2(2-3x)
Рассматриваем данную функцию по частям:
1)y= e^√x
В степени стоит выражение √x и оно похоже на функцию,график которой и есть та самая кривая с область определения D(f)∈[0;+∞)
Поэтому область определения y= e^√x и есть D(f)∈[0;+∞)
2)y= e^log2(2-3x)
В степени стоит выражение log2(2-3x) и найдём у этого выражения область определения так:
Логарифм-функция y=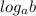 может существовать,если b>0
может существовать,если b>0
Поэтому промежутот является D(f)∈(0;+∞) областью определения.
Отталкиваясь от наших выводов запишем неравенство:
2-3x>0
Решаем и получаем:
x<2/3
D(f) y= e^log2(2-3x) является промежуток : D(f)∈(-∞;2/3)
В итоге построим ось x объединяя все наши расчеты:
----------*0-------------------°2/3--------->x
Получаем,что область определения функции является промежуток :
D(f)∈[0;2/3)
Где * и ° - невыколотая и выколотая точка
3) y= arccos(x-2)-ln(x-2)
Рассматриваем данную функцию по частям:
1)y= arccos(x-2)
В функции есть обратная тригон. функция y=arccos (x).
Вспомним,что область определения такой функции является:
D(f)∈(-1;1)
Поэтому функция y=arccos(x-2) будет смещена,а поэтому область определения будет смещена.
Запишем такой неравенство используя область определения y=arcsin (x):
-1≤x-2≤1
Решаем неравенство через систему:
И получаем:
x≥-1 ; x≤3
Тогда D(f)∈[-1;3]
2) y=ln(x-2)
Натуральный логарифм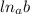 ,как и обычный логарифм имеет свойство,что b>0
,как и обычный логарифм имеет свойство,что b>0
Используя свойство логарифмов составим неравенство:
x-2>0
x>2
В итоге область определения этой функции:
D(f)∈(2;+∞)
Построим ось x объединяя все наши расчеты:
------------*-1--------------------°2-------------*3--------------->x
Область определения y= arccos(x-2)-ln(x-2):
D(f)∈(2;3]
Где * и ° - не выколотая и выколотая точка