1. Математика
  2. Восемнадцатыйрешите уравнение

Восемнадцатый
решите уравнение

DoraDreamer DoraDreamer    3   04.08.2022 07:56    0

Ответы
СавелийРямов СавелийРямов  04.08.2022 07:57

\displaystyle\frac{1}{4}

Пошаговое объяснение:

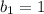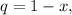
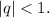
Рассмотрим содержимое больших скобок в левой части уравнения как бесконечно убывающую геометрическую прогрессию с {b_1} = 1 и q = 1 - x,\left| q \right| < 1.

Тогда ее сумма

S = \displaystyle\frac{{{b_1}}}{{1 - q}} = \displaystyle\frac{1}{{1 - (1 - x)}} = \displaystyle\frac{1}{{1 - 1 + x}} = \displaystyle\frac{1}{x},

и данное уравнение можно переписать так:

{x^3} \cdot \displaystyle\frac{1}{x} = \displaystyle\frac{{17}}{4}x - 1;

{x^2} - \displaystyle\frac{{17}}{4}x + 1 = 0;

4{x^2} - 17x + 4 = 0.

Дискриминант этого квадратного уравнения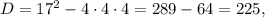 D = {17^2} - 4 \cdot 4 \cdot 4 = 289 - 64 = 225, откуда

x = \displaystyle\frac{{17 \pm 15}}{8}, {x_1} = 4, {x_2} = \displaystyle\frac{1}{4}.

Так как по условию задачи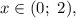 x \in (0;\,\,2), полученный корень 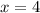x = 4 — посторонний.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Notch Notch  22.06.2019 04:20
Длина аллеи составляет одну четвёртую часть километра.через каждые 50 м с двух сторон аллеи стоят скамейки.сколько скамеек на аллее?...
galinadik84 galinadik84  22.06.2019 04:20
Во вторник в ателье сшили 11 одинаковых курток,а в среду таких же 13 курток.всего на них израсходовали 72 м ткани.сколько метров в каждый из этих дней?...
Дарья122004 Дарья122004  22.06.2019 04:20
Мама дала саше 200 р. и попросила купить молока,кефира и сметану. саша решил купить 2 пакета молока по 32 р., 3 пакета кефира по 27 р. и банку сметаны по 28 р.хватит ли у него денег?...
Matthi Matthi  22.06.2019 04:20
Расставь недостающие запятые 45+615+3225=42,39...
Chokoladik Chokoladik  22.06.2019 04:20
Ателье получило 9 рулонов шерстяной ткани,по 36м в каждом.из половины всей ткани сшили 54 одинаковых костюма,а из остальной ткани платья.сколько сшили ткани если на каждое идёт...
mashenkalarchenko mashenkalarchenko  22.06.2019 04:20
Из одного города в противоположных направлениях выехали автобус и грузовик. через 4ч после начала движения расстояние между ними составляло 528 км скорость движения автобуса 58...
Мухамед5Ли Мухамед5Ли  22.06.2019 04:20
Укажи день зимнего солнцестояния для северного полушария...
Kaatja170 Kaatja170  22.06.2019 04:20
Числа 39 46 22 64 48 99 назови те у которых и количество десятков и количество единиц делится на 2 на 3 и на 4...
duplenkokrist9 duplenkokrist9  22.06.2019 04:20
Две черепахи одновременно поползли на встречу друг другу. одна проползла до встречи 12 м, вторая - в 3 раза больше. какое расстояние было между черепахами вначале?...
flygirl1999cool flygirl1999cool  22.06.2019 04:20
Решить с дробями ! 2/5 всего запаса топлива имеют массу 15 т.найдите массу всего топлива. заранее огромное!...

Популярные вопросы