Во сколько раз сумма трехзначных чисел aba и bab больше суммы двузначных чисел ab и ba?
Другие вопросы по теме Математика
Популярные вопросы
- Решите преобразуйте квадрат двучлена в многочлен стандартного...
1 - Запиши выражения и вычисли их значения: 1. делитель 8,а делимое...
2 - 1.-какая война происходила в середине xx века? 2.-запиши даты...
2 - ирландские сеттеры могут быть слепыми в результате действия...
2 - Разобрать слова по составу: сделанный,привлекают,правдивостью....
3 - Составьте 3 предложения: утвердительное,вопросительное,отрицательное....
1 - Найдите модуль разности корней уравнения (х-3)^2=16 надо!...
3 - Какое число надо уменьшить на 28 чтобы получилось число равное...
1 - Зі словами весна скласти чотири речення щоб там були слова прийшла...
3 - Впервый день хрюша съел 16 желудей.во второй-на 5 желудей больше.всего...
3
111/11
Пошаговое объяснение:
запишем числа в виде суммы разрядных слагаемых
ab=10a+b
ba=10b+a
aba=100a+10b+a=101a+10b
bab=101b+10a
запишем суммы
aba+bab=101a+10b+101b+10a=111a+111b=111(a+b)
ab+ba =10a+b+10b+a=11(a+b)
находим отношение
111(a+b)/11(a+b)=111/11
Сумма трёхзначных чисел равна
Сумма двузначных чисел равна
Найдём, во сколько раз сумма трёхзначных чисел больше суммы двузначных чисел .
ответ: в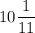 раз .
раз .