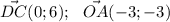Вквадрате abcd сторона равна 6.найдите скалярное произведение векторов dc и oa.
Другие вопросы по теме Математика
Популярные вопросы
- Напишите короткий рассказ по картине «Лунный свет» К. Дебюсси даю 25...
2 - Ужно Употребите данные пословицы как цитаты в составе сложной синтаксической...
2 - Иіндіктің тепе теңдік шарты қандай ответ...
3 - Составить закон распределения дискретной случайной велечины числа попадании...
2 - Знайти довжину медіани BD трикутника ABC, якщо A(1;3),B(-6;3),C(-7;-1)...
1 - Зіставте одяг молоді минулого і сучасності. що вплинуло на зміну моди?...
1 - Выделите цветом верные ответы. О каких обычаях северных народов идёт...
1 - Read and complete the text . There are three choices you don t need...
3 - 1)Я сказал мальчикам, что заблудился, и подсел к ним. (2)Они с меня,...
3 - Визначте роботу, виконану газом при його ізобарному розширенні від...
3
Так как в условии не написано, где находится точка О, будем считать, что это точка пересечения диагоналей.
ABCD - квадрат : AB=BC=CD=AD=6 ⇒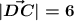
OA - половина диагонали квадрата ⇒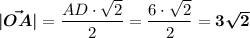
∠A'DC = ∠A'DO + ∠ODC = 90° + 45° = 135°
============================================
Второй координатный.
Разместим квадрат в прямоугольной системе координат, взяв за точку отсчёта вершину А. Так как сторона квадрата равна 6, то точки будут иметь координаты
A(0; 0); B(0; 6); C(6; 6); D(6; 0); O(3; 3)
Тогда координаты векторов