Вероятность появления события А при каждом испытании равна 0,7. Сколько раз достаточно повторить испытание, чтобы с вероятностью 0,9 можно было утверждать, что относительная частота появления события А отклонится от вероятности события А не более, чем на 0,05? ответ: не менее 228 раз. Нужно решение!
Другие вопросы по теме Математика
Популярные вопросы
- Как здесь можно фоткать покажите мне нужно здесь с фоткать отрезок, угол,...
1 - 1)какая в настоящей время самая господствующая группа растений на земле....
3 - Напишите в процентах сколько казахов и др.национальностей проживает в центральном...
2 - Сдано и найти ! рассчитайте массу цинка соответствующую количества вещества...
3 - Солимпиадой как доказать , что лук относится к классу однодольных ?...
3 - Восстановите последовательность нуклеотидов в молекуле днк по предложенной...
1 - Кран піднімає вантаж масою 5 тон на висоту 10 м.потужність двигуна 15 квт.скільки...
2 - Скажите как можно быстрее выучить билеты (по )?...
2 - Записать свои 7 слов безударные (орфография)...
2 - По картинке две коровы одна корова дает 8 литров молока вмести в бидон 18...
3
Вероятность успеха в одном испытании p = 0,7, тогда q = 1-p = 0,3.
По условию, нужно определить n из неравенства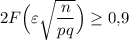 или
или 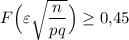
По таблице Лапласа: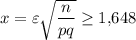
То есть, не менее 228 раз достаточно повторить, что с вероятностью 0,9 можно было утверждать, что относительная частота появления события А отклонится от вероятности события А не более, чем на 0,05