1. Математика
  2. Вектор скорости частицы

Вектор скорости частицы задается уравнением v = 2ti + 3t2j. , где i и j - единичные вектора. Найдите величину вектора перемещения за 2,1 секунд(ы) после начала движения.

valerysidochenozpzmu valerysidochenozpzmu    2   27.02.2021 18:31    2

Ответы
mariyalesnyak mariyalesnyak  29.03.2021 19:33

10.26 (примерно)

Пошаговое объяснение:

Насколько я понял, скорость представлена следующим образом:

\vec{v} = 2t \vec{i} + 3t^2 \vec{j}

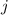Разобьём движение на две составляющих -- вдоль оси i и вдоль j, и будем считать перемещения отдельно для каждых движение, а потом их геометрически сложим.

Для того, чтобы найти перемещение из скорости, возьмём первообразную от скорости. Так как первообразных бесконечно много из-за появляющейся константы, нам нужно гран условие для её поиска. Так как автор вопроса это условие явно не предоставил, я предполагаю, что этим условием является нулевое значение скорости и перемещения при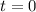 t = 0.

Берём первообразные по обеим осям с нулевой константой:

\vec{S}_i = t^2 \vec{i}      и      \vec{S}_j = t^3 \vec{j}

Складываем оба движения:

\vec{S} = \vec{S}_i + \vec{S}_j = t^2 \vec{i} + t^3 \vec{j}

Значение вектора перемещения в точке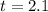 t=2.1:

\vec{S}(2.1) = 4.41 \vec{i} + 9.261 \vec{j}

Чтобы найти абсолютную величину вектора, используем теорему Пифагора для его компонент:

S(2.1) = |\vec{S}(2.1)| = \sqrt{4.41^2+9.261^2} \approx 10.26

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
studentsuka studentsuka  22.08.2019 03:00
Расстояние между двумя пунктами-1840 км. из этих пунктов навстречу друг другу одновремено выехали два поезда.первый поезд проехал пятую восмой, а второй- третью десятую всего пути....
ladysackulina ladysackulina  22.08.2019 03:00
Две водомерки одновременно навстречу друг другу с противоположных берегов озера. одна водомерка скользила по воде 4 мин со скоростью 57м/мин. другая водомерки до встречи расстояние,...
kotizm kotizm  22.08.2019 03:00
Из двух городов,расстояние между которыми 276 км,одновременно в противоположных направлениях выехали 2 машины. скорость одной 75км/что,а другой на 18км/что меньше.на каком расстоянии...
TheAgentSquid TheAgentSquid  22.08.2019 03:00
Вгороде за год должны построить 15000 квартир. за два месяца строители сдали 6 домов, по 198 квартир в каждом , и 5 домов , по 270 квартир в каждой. сколько стоит ещё квартир осталось...
ека29 ека29  22.08.2019 03:00
В7/15 и 5/9 е 5/8 и 2/3 и 3/10 и 33/100 дроби к наименьшему общему знаменателю...
nikas45 nikas45  22.08.2019 03:00
Сочинение на башкирсном про птиц 3 класс...
ударник52 ударник52  22.08.2019 03:00
Одновременно из двух городов навстречу друг другу выехали автомобиль и встретились через 9 2 3 часа первый автомобиль проходит за 14 одну вторую часа за сколько времени пройдет автомобиль...
reprto345mak reprto345mak  22.08.2019 03:00
Водно и тоже время друг другу на встречу из двух городов отправились два поезда . один из них за1/4 часа проходит 13км а второй за1/3часа проходит16км. спустя часа эти поезда встретились....
lolkekcheburek27 lolkekcheburek27  22.08.2019 03:00
Кто нибудь ! не могу решить заранее . 1 3/8+(5/6х-5/6)=2 1/4...
Nymeria Nymeria  22.08.2019 03:00
1)l-47,5 l-l-31,2l= 2)5 1/3*l-1 1/8l+8: l-0,01 обчисліть з модулями будь ласка....

Популярные вопросы