Вариант 1.

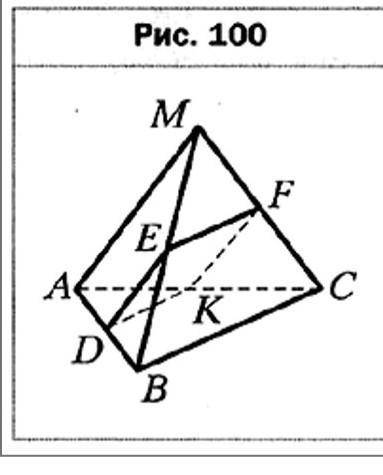
1. Точки D, Е, F и К — середины рёбер АВ, МВ, МС и АС тетраэдра МАВС соответственно, ВС = 42 см, AM = 36 см (рис. 100). Докажите, что точки D, Е, F и К являются вершинами параллелограмма, и вычислите периметр этого параллелограмма.

2. Плоскость β пересекает стороны АС и ВС треугольника АВС в точках Е и F соответственно и параллельна стороне АВ, АЕ : СЕ = 5:2, АВ = 21 см. Найдите отрезок EF.

3. Параллелограмм ABCD является изображением ромба A1B1C1D1, точка М — изображение некоторой точки M1 отрезка C1D1 (рис. 101). Постройте изображение перпендикуляра, опущенного из точки М1 на диагональ B1D1 ромба.

4. Плоскости β и γ параллельны. Из точки А, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости β и γ в точках В1 и С1, а другой — в точках В2 и С2 соответственно. Найдите отрезок С1С2, если он на 14 см больше отрезка В1В2, АС1 =11 см, В1С1 = 7 см.

5. Дан эллипс, являющийся изображением окружности с центром О (рис. 102). Постройте изображение точки О.

​

1. Для доказательства того, что точки D, Е, F и К являются вершинами параллелограмма, можем использовать следующий подход:
- Нам дано, что D - середина ребра АВ. Это означает, что отрезок АD равен отрезку DB (так как D - середина).
- Также дано, что Е - середина ребра МВ. Это означает, что отрезок МE равен отрезку ЕВ.
- Поскольку ВС = 42 см и М - середина ребра СА, то отрезок МС равен отрезку МА, а следовательно, МС = 36 см.
- Кроме того, К - середина ребра АС, поэтому отрезок АК равен отрезку КС.

Итак, мы имеем следующие равенства:
АD = DB
МЕ = ЕВ
МС = 36 см
АК = КС

Чтобы доказать, что точки D, Е, F и К являются вершинами параллелограмма, нужно показать, что стороны параллелограмма параллельны.

Возьмем стороны АD и МЕ:
- АD и МЕ отрезки, концы которых соединяют противоположные вершины (А и М соединены через D, а Е и В соединены через М).
- Так как D и Е являются серединами соответствующих ребер, М прямоугольник ДЕВМ должен быть параллелограммом.
- По определению, параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны.

Поэтому, стороны АD и МЕ являются параллельными.

Теперь рассмотрим стороны МС и АK:
- МС и АК отрезки, концы которых соединяют противоположные вершины (М и В соединены через К, а А и С соединены через М).
- Так как К и С являются серединами соответствующих ребер, АК прямоугольник КСАМ должен быть параллелограммом.
- По определению, параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны.

Поэтому, стороны МС и АК являются параллельными.

Теперь мы доказали, что все стороны параллелограмма АDМЕ - параллельны. Чтобы вычислить его периметр, нужно сложить длины всех его сторон.

Периметр параллелограмма АDМЕ:
AD + DM + ME + EA = (AD + DM + MA + AE) (так как МС = 36 см и КС = АК)

Мы знаем, что AD = DB, DM = МС, MA = МС и AE = ВЕ, так как D, Е, F и К - середины соответствующих ребер.

Подставим известные значения:
(AD + DM + MA + AE) = (DB + МС + МС + ВЕ)

Так как ВС = 42 см и AM = 36 см, можно заметить, что ВЕ = ВС - АМ = 42 - 36 = 6 см.

Подставим это значение и рассчитаем периметр:
(DB + МС + МС + ВЕ) = (DB + МС + МС + 6)

В задаче не дано значения DB, поэтому невозможно точно рассчитать периметр. Мы можем только выразить его в терминах DB и МС.

2. Для нахождения отрезка EF, рассмотрим следующее:
- Е и F - точки пересечения плоскости β с сторонами АС и ВС треугольника АВС соответственно.
- Плоскость β параллельна стороне АВ, поэтому угол ЕАС должен быть равен углу СЕF.
- Из условия дано, что АЕ : СЕ = 5 : 2.
- Поэтому можно сделать вывод, что угол ЕАС больше угла СЕF в отношении 5 : 2.
Если мы обозначим угол ЕАС как x, то угол СЕF будет равен (2/5) * x.

В треугольнике АВС сумма углов равна 180 градусам:
Угол А + Угол В + Угол С = 180
(x) + (180 - x - (2/5) * x) + ((2/5) * x) = 180

Решим уравнение:
x + 180 - x - (2/5) * x + (2/5) * x = 180
Упростим:
x - (2/5) * x + (2/5) * x = 0
(3/5) * x = 180 - 180
(3/5) * x = 0

Умножим обе части на 5/3:
x = 0 * (5/3)
x = 0

Таким образом, угол ЕАС равен 0 градусов.
Из-за этого отрезок EF будет равен 0.

3. Чтобы построить изображение перпендикуляра, опущенного из точки М1 на диагональ B1D1 ромба, нужно следовать этим шагам:
- Возьмите отрезок B1D1 и найдите его середину (назовем ее R).
- Проведите прямую, проходящую через точку M1 и перпендикулярную отрезку B1D1 (эта прямая будет пересекать отрезок B1D1 в точке S).
- Точка S будет проекцией точки М1 на диагональ B1D1 ромба.

4. Для нахождения отрезка С1С2, нужно рассмотреть следующее:
- Известно, что С1С2 - 14 см больше, чем В1В2.
- Также известно, что АС1 = 11 см и В1С1 = 7 см.

Мы можем использовать теорему Пифагора, чтобы найти отрезок С1С2.
Согласно теореме Пифагора, сумма квадратов длин катетов равна квадрату длины гипотенузы.

Обозначим отрезок В1С2 как х:
(В1С1)² + (С1С2)² = (В1С2)²

Подставим известные значения:
(7)² + (С1С2)² = (х)²

(49) + (С1С2)² = (х)²

Мы знаем, что С1С2 = В1В2 + 14. Подставим это в уравнение:
(49) + ((В1В2) + 14)² = (х)²

Мы также знаем, что В1С1 = 7 см и АС1 = 11 см:
В1С2 = В1С1 + С1С2 = В1С1 + (В1В2 + 14)

Подставим это значение в уравнение:
(49) + ((В1С1 + (В1В2 + 14)) + 14)² = (х)²

Подставим известные значения В1С1 = 7 см и АС1 = 11 см:
(49) + ((7 + (В1В2 + 14)) + 14)² = (х)²

(49) + ((21 + В1В2) + 14)² = (х)²

Теперь мы имеем уравнение, которое можно решить, используя известные значения В1В2. Подставьте значение В1В2 и решите уравнение, чтобы найти отрезок С1С2.

5. Задача не дает достаточно информации для построения точки О, являющейся центром окружности и, соответственно, центра эллипса на изображении. Нам нужна информация о размерах и положении эллипса относительно других элементов рисунка.