ів за 3 приклади!
До іть будь ласка, обчислити площі фігур, обмежених лініями:

Ответы

ArianaZimanina 04.08.2022 10:12

а) $\displaystyle\frac{32}{3};$ б) 2; в) $\displaystyle\frac{{15{a^2}\pi }}{{32}}$

Пошаговое объяснение:

а) Найдем точки пересечения указанных графиков $y = f(x) = {x^2}$ и y = g(x) = 4x (рис. 1), приравняв правые части:

${x^2} = 4x,$

${x^2} - 4x = 0,$

x(x - 4) = 0,

$x = 0,\, x = 4.$

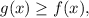Так как на промежутке $[0;\,\,4]$ $g(x) \ge f(x),$ то применяя формулу Ньютона-Лейбница, получаем

$S = \int\limits_0^4 {(g(x) - f(x))dx} = \int\limits_0^4 {(4x - {x^2})dx} = =\left. {\left( {\displaystyle\frac{{4{x^2}}}{2} - \displaystyle\frac{{{x^3}}}{3}} \right)} \right|_0^4 = 2 \cdot {4^2} - \displaystyle\frac{{{4^3}}}{3} = 32 - \displaystyle\frac{{64}}{3} = \displaystyle\frac{{32}}{3}.$

б) Нарисуем в одной координатной плоскости все указанные линии и заштрихуем область, площадь которой необходимо найти. Разобьем получившуюся фигуру на две части прямой x = 1 (рис. 2).

Тогда левая часть фигуры — квадрат со стороной 1, его площадь равна 1.

Площадь правой части фигуры найдем как площадь криволинейной трапеции, ограниченной графиком функции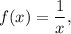 $f(x) = \displaystyle\frac{1}{x},$ прямыми y = 0, x = 1 и x = e, используя формулу Ньютона-Лейбница:

$\int\limits_1^e {f(x)dx} = \int\limits_1^e {\displaystyle\frac{{dx}}{x}} = \left. {\ln x} \right|_1^e = \ln e - \ln 1 = 1.$

Таким образом, площадь заданной фигуры равна 1 + 1 = 2.

в)

$\rho = a{\sin ^3}\displaystyle\frac{\varphi }{3}.$

(рис. 3 для случая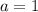 a = 1 ).

Решаем неравенство

$a{\sin ^3}\displaystyle\frac{\varphi }{3} \ge 0,$

$\sin \displaystyle\frac{\varphi }{3} \ge 0,$

$\displaystyle\frac{\varphi }{3} \in [\pi k;\,\,\pi + \pi k],\\$

$\varphi \in [3\pi k;\,\,3\pi + 3\pi k].$

Для вычисления площади криволинейного сектора воспользуемся формулой

$S = \displaystyle\frac{1}{2}\int\limits_a^b {{p^2}(\varphi )d\varphi } .$

Из формулы синуса тройного угла следует, что

${\sin ^3}x = \displaystyle\frac{{3\sin x - \sin 3x}}{4}.$

Тогда

${\sin ^6}x = \displaystyle\frac(3\sin x - \sin 3x)}^2}}}{{{4^2}}} = \displaystyle\frac{{9{{\sin }^2}x - 6\sin x\sin 3x + {{\sin }^2}3x}}{{16}}.$

Понижая степень синуса и записывая произведение синусов в виде суммы, получим

$\[{\sin ^6}x = \displaystyle\frac{{9 \cdot \left( {\displaystyle\frac{{1 - \cos 2x}}{2}} \right) - 6 \cdot \displaystyle\frac{1}{2}(\cos (3x - x) - \cos (3x + x)) + \displaystyle\frac{{1 - \cos 6x}}{2}}}{{16}} =$

$=\displaystyle\frac{{\displaystyle\frac{9}{2} - \displaystyle\frac{9}{2}\cos 2x - 3\cos 2x + 3\cos 4x + \displaystyle\frac{1}{2} - \displaystyle\frac{1}{2}\cos 6x}}{{16}} =$

$=\displaystyle\frac{5}{{16}} - \displaystyle\frac{{15}}{{32}}\cos 2x + \displaystyle\frac{3}{{16}}\cos 4x - \displaystyle\frac{1}{{32}}\cos 6x.$

Тогда площадь

$S = \displaystyle\frac{1}{2}\int\limits_0^{3\pi } {{{\left( {a{{\sin }^3}\displaystyle\frac{\varphi }{3}} \right)}^2}d\varphi } = \displaystyle\frac{{{a^2}}}{2}\int\limits_0^{3\pi } {{{\sin }^6}\displaystyle\frac{\varphi }{3}d\varphi } =$ $= \displaystyle\frac{{{a^2}}}{2}\int\limits_0^{3\pi } {\left( {\displaystyle\frac{5}{{16}} - \displaystyle\frac{{15}}{{32}}\cos \displaystyle\frac{{2\varphi }}{3} + \displaystyle\frac{3}{{16}}\cos \displaystyle\frac{{4\varphi }}{3} - \displaystyle\frac{1}{{32}}\cos 2\varphi } \right)d\varphi } =$

$= \left. {\displaystyle\frac{{{a^2}}}{2}\left( {\displaystyle\frac{{5\varphi }}{{16}} - \displaystyle\frac{{15}}{{32}} \cdot \displaystyle\frac{3}{2}\sin \displaystyle\frac{{2\varphi }}{3} + \displaystyle\frac{3}{{16}} \cdot \displaystyle\frac{3}{4}\sin \displaystyle\frac{{4\varphi }}{3} - \displaystyle\frac{1}{{32}} \cdot \displaystyle\frac{1}{2}\sin 2\varphi } \right)} \right|_0^{3\pi } =$