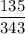1. Математика
  2. В урне находятся 3 шара белого

В урне находятся 3 шара белого цвета и 4 шара черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется: не менее двух белых шаров.

rostikstorozhev rostikstorozhev    3   03.07.2020 17:58    1

Ответы
Kimaru110 Kimaru110  19.08.2020 06:17

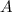Пусть A — событие, состоящее в том, что шар наудачу извлекается и возвращается в урну три раза.

Имеем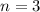 n=3 одинаковых независимых события, в каждом из которых то самое событие 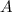A совершается с некоторой вероятностью 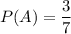P(A) = \dfrac{3}{7} и не совершается с одинаковой вероятностью 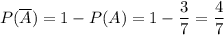P(\overline{A})= 1 - P(A) = 1 - \dfrac{3}{7} = \dfrac{4}{7}. Такую совокупность условий называют схемой Бернулли.

Вероятность того, что в схеме Бернулли событие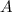 A совершится ровно 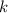k раз, обозначают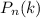 P_{n}(k)

Теорема Бернулли: в схеме Бернулли с параметрами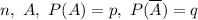 n, \ A, \ P(A)=p, \ P(\overline{A})=q справедливо равенство 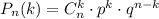P_{n}(k) = C^{k}_{n} \cdot p^{k} \cdot q^{n-k}. Это равенство называют формулой Бернулли.

Для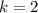 k = 2 имеем:

P_{3}(2) = C^{2}_{3} \cdot \left(\dfrac{3}{7} \right)^{2} \cdot \left(\dfrac{4}{7} \right)^{3-2} = \dfrac{3!}{(3-2)! \cdot 2!} \cdot \dfrac{9}{49} \cdot \dfrac{4}{7} = \dfrac{108}{343}

Поскольку в задаче стоит найти вероятность того, что среди извлеченных шаров окажется не менее двух белых шаров, то рассмотрим вероятность выбора 3 белых шаров из 3 попыток.

Для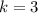 k = 3 имеем:

P_{3}(3) = C^{3}_{3} \cdot \left(\dfrac{3}{7} \right)^{3} \cdot \left(\dfrac{4}{7} \right)^{3-3} = \dfrac{27}{343}

Имеем два несовместимых события, поэтому:

P(A) = P_{2}(3) + P_{3}(3) = \dfrac{108}{343} + \dfrac{27}{343} = \dfrac{135}{343}

ответ: \dfrac{135}{343}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Tini2311 Tini2311  14.07.2019 06:10
20*(0,7б) преобразуй те в тождественно равные выражение...
AsassinGirl AsassinGirl  14.07.2019 06:10
Оч важно! (25 ) по ломанной ксва, длина которой равна 54 см, ползет волшебный муравей. за первую минуту он проползает звено кс, равное 9 2 15 см, за следующую минуту...
ViNtIk4312 ViNtIk4312  14.07.2019 06:10
Большое горе, беда для многих людей. 9 букв, первая буква т , четвёртая буква г и предпоследняя буква и ....
vovasherbak2003 vovasherbak2003  14.07.2019 06:10
Используя распределительное свойство умножения вычислите значение проиведения 1)5×(-107),2)-9×101,)×103...
ниро4 ниро4  14.07.2019 06:10
Впервый день отрезали 6м ткани во второй на 2м меньше чем в первый а в третий на 4 больше чем во второй сколько метров отрезали в третий день...
TASHER228YMMlol TASHER228YMMlol  14.07.2019 06:10
Площадь прямоугольника равна 24, а его стороны относятся как 2: 3. чему равна диагональ прямоугольника...
Жания27 Жания27  14.07.2019 06:10
Сообщение записано с двоичного кода.его длина 4096 символов.к аков обьем этого сообщения в килобайтах?...
nikita540601 nikita540601  14.07.2019 06:10
На экскурсию в музей на кондитерскую фабрику поехали 30 учеников 5 часть всех детей поехала в музей остальные на кондитерскую фабрику сколько учеников поехала в музей...
daqqwe daqqwe  14.07.2019 06:10
Реши : петя начертил ломануюлинию из двух звеньев.длина первого звена 8 см,а второго 5 см.антон тоже начертил ломаную линию,но из трех звеньев.длина первого и второго...
dashazoriksv dashazoriksv  14.07.2019 06:10
Поставьте вопрос к так,чтобы она решалась с сложения. гуси улетают в теплые страны в октябре,а возвращаются в апреле....

Популярные вопросы