1. Математика
  2. В треугольнике MNK MN=10cм, NK=20см,

В треугольнике MNK MN=10cм, NK=20см, угол N равен 98 градусов Надо найти:
1. длину стороны MK
2. углы M и K
3. площадь треугольника MNK
4. периметр тр-ка MNK
5. длину высоты NS

lolipop1720 lolipop1720    1   07.08.2022 04:29    0

Ответы
жандосЕУ жандосЕУ  07.08.2022 06:00

1.\ 23{,}6.\\2.\ 57^\circ,\, 25^\circ;\\3.\ 99;\\ 4.\ 53{,}6\\ 5.\ 8{,}4

Пошаговое объяснение:

1) По теореме косинусов из треугольника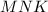 MNK

M{K^2} = M{N^2} + N{K^2} - 2MN \cdot NK\cos \angle MNK;

M{K^2} = {10^2} + {20^2} - 2 \cdot 10 \cdot 20\cos 98^\circ ;

M{K^2} = 100 + 400 - 400\cos 98^\circ ;

M{K^2} = 500 - 400\cos 98^\circ ;

MK = \sqrt {100(5 - 4\cos 98^\circ )} ;

MK = 10\sqrt {5 - 4\cos 98^\circ } .

Вычисляем найденное значение приблизительно с калькулятора. Тут и далее будем округлять значения тригонометрических функций до сотых, сторон — до десятых, углов — до единиц.

\cos 98^\circ \approx - 0{,}14,

тогда

5 - 4\cos 98^\circ \approx 5 - 4 \cdot ( - 0{,}14) = 5 + 0{,}56 = 5{,}56;

\[MK \approx 10\sqrt {5{,}56} \approx 10 \cdot 2{,}36 = 23{,}6.\]

2) По теореме синусов

\displaystyle\frac{a}{{\sin \alpha }} = \displaystyle\frac{b}{{\sin \beta }} = \displaystyle\frac{c}{{\sin \gamma }}

найдем синусы одного из недостающих углов, а значит и сам этот угол.

\displaystyle\frac{{MK}}{{\sin \angle N}} = \displaystyle\frac{{NK}}{{\sin \angle M}};

\displaystyle\frac{{23{,}6}}{{\sin 98^\circ }} = \displaystyle\frac{{20}}{{\sin \angle M}},

откуда

\sin \angle M = \displaystyle\frac{{20\sin 98^\circ }}{{23{,}6}} \approx \displaystyle\frac{{20 \cdot 0{,}99}}{{23{,}6}} \approx 0{,}84,\ \angle M \approx 57^\circ ;

Тогда третий угол

\angle K \approx 180^\circ - (98^\circ + 57^\circ ) = 180^\circ - 155^\circ = 25^\circ .

3) Площадь треугольника найдем по формуле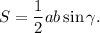 S = \displaystyle\frac{1}{2}ab\sin \gamma .

S = \displaystyle\frac{{MN \cdot KN}}{2}\sin 98^\circ \approx \displaystyle\frac{{10 \cdot 20}}{2} \cdot 0{,}99 = 99.

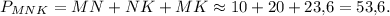
4) {P_{MNK}} = MN + NK + MK \approx 10 + 20 + 23{,}6 = 53{,}6.

5)  Длину высоты найдем через площадь. Так как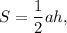 S = \displaystyle\frac{1}{2}ah, то h = \displaystyle\frac{{2S}}{a}.

NS = \displaystyle\frac{{2S}}{{MK}} \approx \displaystyle\frac{{2 \cdot 99}}{{23{,}6}} \approx 8{,}4.


В треугольнике MNK MN=10cм, NK=20см, угол N равен 98 градусов Надо найти: 1. длину стороны MK 2. уг
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
kristinavasina1 kristinavasina1  21.05.2020 16:07
Грузовик вес 1983тонны песка. Другой грузовик в 5 раз больше, а третий в 198раз больше первого и второго грузовика вместе. Сколько всего тонн везли три грузовика?...
Vlarizon98 Vlarizon98  21.05.2020 16:07
В фермерском хозяйстве 2 га заняты усадьбой и постройками, под посевами — 370 га, под сенокосом — 330 га, под лесом — 20 га и под выгоном — 120 га. Сколько всего земли в пользовании...
omon3565 omon3565  21.05.2020 16:07
До ть будь ласка ів!!Дано: KA=KB кут AKP = BKPДовести: трикут. KAP = KBP​...
polycov200412 polycov200412  21.05.2020 16:07
Мальчик прочитал 78 страниц(-ы), что составляет 13 % числа всех страниц в книге. Сколько страниц в книге?...
svetysa95 svetysa95  21.05.2020 16:07
Решение уровня x-38=77 62- x=45...
jjjghhgg6 jjjghhgg6  21.05.2020 16:07
Вычислить: а)|3,5|+|7,9| б) |5,12|+|-6,11| в) |-11,3|-|-1,9| Очень надо...
Тотах Тотах  21.05.2020 16:07
134 умножить на 4 как решаеться...
shishkinaviolet shishkinaviolet  21.05.2020 16:07
математика, переводится ли эта дробь в десятичную? если да то переведите: 79/2760...
корги1 корги1  21.05.2020 16:07
В первый день магазин продал 3/5 тонны овощей, а во второй день на 1/10 тонны меньше. Сколько овощей продал магазин за два дня?​...
MuclePan MuclePan  21.05.2020 16:07
В зале 120 мест. Две трети уже заняты. Сколько зрителей ещё может занять свободные места?...

Популярные вопросы