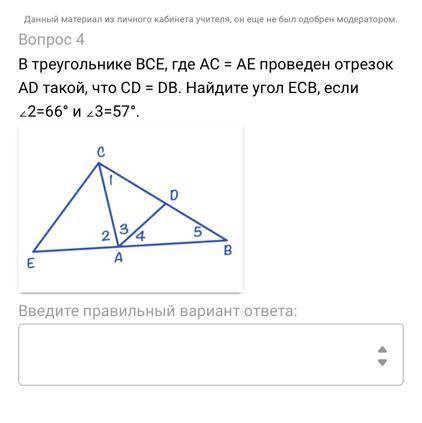
В треугольнике BCE, где AC = AE проведен отрезок AD такой, что CD = DB. Найдите угол ECB, если ∠2=66° и ∠3=57°.
Другие вопросы по теме Математика
Популярные вопросы
- Решите это , у меня всего 40мин!...
2 - Майкл Х.Харт «100 ұлы адам» атты кiтабынан – «Альберт Эйнштейн»....
1 - Довжига кімнати 4,2 м, а ширина 3,3 метра....
1 - Қазақ тілі 5 сынып БЖБ 2-тапсырмасы міне көмектесіңішші...
3 - Завершите уравнения реакций...
3 - очень нужно сор осталось времени 30мин...
3 - Рассмотрите картинку и выполните задание:СОЛНЕЧНАЯ СИСТЕМА Задание...
3 - К окружности с центром O проведена касательная CD (D - точка касания)....
2 - Rewrite the sentences using the words in brackets. 1.It’s possible...
2 - В стеклянный блок попадает луч света АВ и ломается. Поломка стеклапоказатель...
2
123 градуса
Пошаговое объяснение:
123
Пошаговое объяснение:
Поскольку AC=AE, это означает, что треугольник ABC равнобедренный.
Также, из условия CD = DB, мы знаем, что отрезок AD является медианой треугольника ABC.
Из свойств медианы, мы знаем, что она разделяет треугольник на две части, которые равны между собой. Это означает, что площадь треугольника ACD равна площади треугольника ADB.
Так как треугольники ACD и ADB имеют общую высоту, которая проведена к основанию AD, площадь каждого треугольника пропорциональна его основанию.
Обозначим площадь треугольника ACD через S1, а площадь треугольника ADB через S2.
Поскольку площади треугольников равны, можно записать следующее уравнение:
S1 = S2
Так как площадь треугольника равна половине произведения основания на высоту, можно записать выражения для площадей треугольников:
S1 = (AC * AD) / 2
S2 = (AE * AD) / 2
Используя эти равенства, мы можем записать следующее:
(AC * AD) / 2 = (AE * AD) / 2
Упрощая уравнение, убирая общий множитель и деля на AD, мы получаем:
AC = AE
Таким образом, мы можем заключить, что треугольник ACE равнобедренный.
Теперь рассмотрим треугольник BCE.
У нас уже есть два угла из этого треугольнике: ∠2 = 66° и ∠3 = 57°.
Мы знаем, что сумма всех углов в треугольнике равна 180°.
Поэтому мы можем записать уравнение:
∠ECB + ∠2 + ∠3 = 180°
Подставляем известные значения:
∠ECB + 66° + 57° = 180°
Складываем числа и получаем:
∠ECB + 123° = 180°
Теперь вычитаем 123° из обеих частей уравнения:
∠ECB = 57°
Таким образом, угол ECB равен 57°.