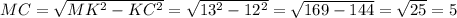В треугольнике АВС угол с-90 АС-15 ВС-20 из точки М к плоскости треугольника проведён перпендикулярно СМ расточения до точки М до стороны АВ-13 найдитедлину МС
Другие вопросы по теме Математика
Популярные вопросы
- Отметь, какие отрезки являются диаметрами окружности....
3 - 1. Какие проблемы ставит автор в рассказе Скупой рыцарь (Елена Долгопят)...
2 - Каким образом можно изменить упругие свойства тел? Приведите примеры...
2 - БЕСПЛАТНЫЕ АЛГЕБРА 7 КЛАСС...
2 - Определи объём чугунной детали, если её вес составляет 481 H....
1 - Выберите три правильных ответа 1) Фотосистема II характеризуется следующими...
2 - 12. Формула речовини складається з Натрію й Сульфуру. вiдомими валентностями...
2 - Выпиши из предложений дополнение с главным словом, задай к дополнению вопрос. Определи,...
1 - СРОНО !! - Название сказки - Морожены песни. Вопрос - Чем эта сказка похожа...
2 - ,сделайте это задание( все 4 пункта) Надеюсь на ваш адекватный ответ....
1
MC = 5
Пошаговое объяснение:
Дано: ∠ACB = 90°, AC = 15, BC = 20, CM ⊥ ABC, MK = 13, MK ⊥ AB
Найти: MC - ?
Решение: Так как треугольник ΔABC - прямоугольный(∠ACB = 90° по условию), то по теореме Пифагора: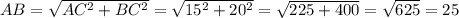
По теореме про три перпендикуляра CK ⊥ AB, так как по условию CM ⊥ ABC, MK ⊥ AB. По формулам площади для треугольника ΔABC:
AC * BC * 0,5 = CK * AB * 0,5|:0,5
AC * BC = CK * AB |:AB
Рассмотри треугольник ΔMKC, который является прямоугольным так как CM ⊥ ABC по условию, тогда по теореме Пифагора: