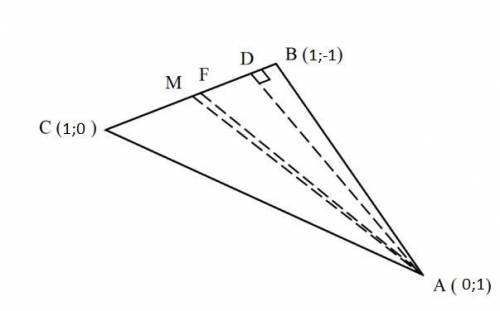
В треугольнике АВС найти А(x1; y1) = (0; 1), B(x2; y2) = (1; ­1) , C(x3; y3) = (1; 0): 1) уравнение стороны ВС;
2) величину угла при вершине А;
3) уравнение и длину высоты к стороне ВС;
4) уравнение и длину медианы к стороне ВС;
5) уравнение биссектрисы угла при вершине А;
6) площадь треугольника АВС.

1) Длина стороны ВС равна √((Xc-Xb)²+(Yc-Yb)²) = √((17-1)²+(2-0)²) =

    = √(16²+2²) = √(256+4) = √260 = 2√65 = 16.1245.

   Аналогично находим  длину стороны АВ = 5, и АС = 13.

2) Площадь S = (1/2)*|(Xb-Xc)*(Yc-Ya)-(Xc-Xa)*(Yb-Ya)| =

    = (1/2)*|(1-5)*(2-(-3))-(17-5)*(0-(-3))| = (1/2)*|-4*5-12*3| =(1/2)|-56| = 28.

3) Уравнение стороны ВС: 

    (X-Xb)/(Xc-Xb) = (Y-Yb)/(Yc-Yb)

   (X-1)/(17-1) = (Y-0)/(2-0)

    (X-1)/16 = Y/2

     X-8Y-1=0    или с коэффициентом: У = (1/8)X - (1/8).

4) Уравнение высоты из вершины А:

     (Х-Xa)/(Yc-Yb) = (Y-Ya)/(Xb-Xc)

     (X-5)/(2-0) = (Y-(-3))/(1-17)

     (X-5)/2 = (Y+3)/-16

      8X+Y-37=0     или Y = -8X+37.

    Аналогично находим уравнения высоты из вершины В:

   12Х+5У-12=0,

    и из вершины С:

    4Х-3У-62=0.

5) Высота из вершина А равна Ha = 2S/BC = 2*28 / 2√65 = 3,473.

    Из вершины В: Нв = 2*28 / 13 = 4,308.

    Из вершины С: Нс = 2*28 / 5 = 11,2.

6) Косинус угла В: cosB = (AB²+BC²-AC²) / (2*AB*BC) =

     = (5²+(2√65)²-13²) / (2*5*2√65) = 116/20√65 = 

0.7194

Угол В = 0.76786 радиан = 

43.9949 градуса.