1. Математика
  2. В треугольнике АВС биссектриса

В треугольнике АВС биссектриса АТ, перпендикулярная медиане ВМ пересекает ее в точке Р. Найдите сторону ВС, если A = 60° и PM=8 см

димон7777 димон7777    2   29.07.2022 20:59    0

Ответы
GromovaRus GromovaRus  29.07.2022 22:00

16\sqrt 3

Пошаговое объяснение:

В треугольнике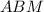 ABM биссектриса 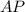AP одновременно является высотой, следовательно, этот треугольник равнобедренный, 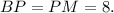BP = PM = 8. Поскольку угол при его вершине равен 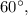60^\circ , он равносторонний,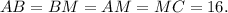 AB = BM = AM = MC = 16.

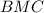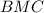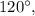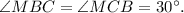
Так как треугольник BMC равнобедренный и угол BMC равен 120^\circ , то \angle MBC = \angle MCB = 30^\circ .

Таким образом,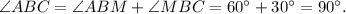 \angle ABC = \angle ABM + \angle MBC = 60^\circ + 30^\circ = 90^\circ .

Тогда BC = AB{\mathop{\rm ctg}\nolimits} 30^\circ = 16\sqrt 3.


В треугольнике АВС биссектриса АТ, перпендикулярная медиане ВМ пересекает ее в точке Р. Найдите стор
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
444477 444477  27.08.2019 02:20
1м24дм-7дм 80мм2= 6 га 71 а+34га29 а= 21км 48 м: 6= 15 ч 30 минумножить на 8 =...
ната5810 ната5810  27.08.2019 02:20
Срешением,уже мозги закипают. для 5 класса.в 1 день было изготовлено 5/18 заказанных деталей, во 2- 7/24.после того,как в 3 день сделали 18/31 деталей,которые остались изготовить,остаток...
ged95 ged95  27.08.2019 02:20
1/4 + 2/3 1/3 + 3/4 возможные ответы: 11/13 | 12/13 | 17/7 | 7/17 | 13/12...
Корни Корни  27.08.2019 02:20
Вмагазин 6 ящиков слив по 19 кг в каждом 7 ящиков яблок по 15 кг сколько кг фруктов в магазин...
sens1980 sens1980  27.08.2019 02:20
Почему чувства, по мнению большинства античных философов, не могут служить критерием истины...
ZloYDedyskA ZloYDedyskA  27.08.2019 02:20
Возможные ответы: 88 | 45 | 60 | 2 | 12 : нок (64 ; 88) нод (64 ; 88)...
Romabl4 Romabl4  27.08.2019 02:20
Найдти среднюю скорость машины ,если расстояние до остановки 300 км она ехала 5 часов потом 3 часа стояла потом двигалась дальше до расстояния 500 км .весь путь с остановкой =15...
valwkebe valwkebe  27.08.2019 02:20
Площадь треугольника abc=24см.на стороне abобозначили точки d и f так что, ad=bf=1/4ab, а на стророне bc точки p,m так что cm=bp=1/4bc.найти площадь четырехугольника dfpm...
KiloMETR1336 KiloMETR1336  27.08.2019 02:20
Денис загадал число. он умножил свое число на -10, прибавил к результату -0,7, разделил полученное число на 2/3 и получил -1,2. какое число загадал денис?...
oksankavdovina oksankavdovina  27.08.2019 02:20
Найди значение выражений 23-18/3+36 8+(24-16)*3 150-64/8+2*4...

Популярные вопросы