1. Математика
  2. В треугольнике ABC угол

В треугольнике ABC угол C прямой. Известно, что BC=12, CA=5. Пусть I— точка пересечения биссектрис. Найдите расстояние от I до AB

Арпинэ1 Арпинэ1    1   16.03.2020 06:06    5

Ответы
planeta88 planeta88  11.10.2020 22:52

Точка пересечения биссектрис является центром вписанной окружности, расстояние от точки \sf I до \sf AB это есть радиус вписанной окружности.

Найдем гипотенузу прямоугольного треугольника, по т. Пифагора

\sf AB=\sqrt{12^2+5^2}=13

Искомое расстояние: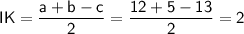 \sf IK=\dfrac{a+b-c}{2}=\dfrac{12+5-13}{2}=2

ответ: 2.


В треугольнике ABC угол C прямой. Известно, что BC=12, CA=5. Пусть I— точка пересечения биссектрис.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
89186119688 89186119688  15.09.2019 05:20
Стену длиной 6 м и высотой 3 м хотят выложить кафелем. одна кафельная плитка имеет форму квадрата со стороной 15 см , а в одном ящике -150 плиток . какое наименьшее...
Plild Plild  15.09.2019 05:20
Длинна 1 стороны треугольника -8см 6мм.2 сторона треугольника-5 см 8 мм,периметр-19 см, 3 сторона -? построй отрезок длинна которого равна длинне трех старон треугольника...
vladsunygin vladsunygin  15.09.2019 05:20
Айдар и жания пошли в сад, чтобы собрать вишню.айдар собирает ведро вишни за 2 ч, а жания за 3 ч. за какое время они соберут одно ведро вместе?...
ndjfhfidi ndjfhfidi  15.09.2019 05:20
Пассажир был в пути двое суток и ещё треть суток. сколько всего часов был пассажир в пути?...
pointbreakk9 pointbreakk9  15.09.2019 05:20
Решите уравнение объясните как: с (12х-+5)=32...
380931817787 380931817787  15.09.2019 05:20
Школьник прочитал книгу за 3 дня, в первый день он прочитал 1/5 , во второй день 5/8 остатка и в третий день 1/3 нового остатка и последние 16 страниц. сколько...
elenanovikova21 elenanovikova21  15.09.2019 05:20
Решите уравнение (8--4х)=17 объясните как : с...
Olka1909 Olka1909  15.09.2019 05:20
Составить уравнение линии, для каждой точки которой ее расстояние до точки a(x1; y1) равно расстоянию до прямой y = b. полученное уравнение к простейшему виду и...
galinarezeda59 galinarezeda59  15.09.2019 05:20
Начертитьпрямоугольник,у которого 2 угла прямые,а 1-тупой....
lida20171 lida20171  15.09.2019 05:20
Стрелок,имея 4 патрона,стреляет по цели до первого попадания или до израсходования всех патронов.составить закон распределения числа произведенных выстрелов,если...

Популярные вопросы