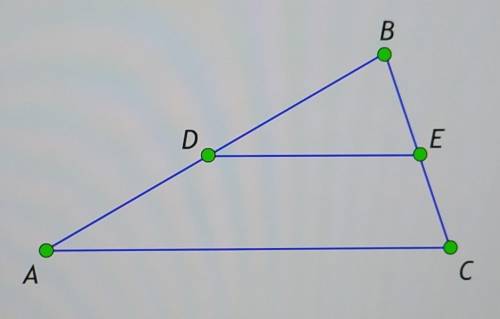
В треугольнике ABC провели среднюю линию DE. Площадь трапеции ADEC равна 6. Определите площадь треугольника ABC.​

Для решения задачи, нам понадобятся знания о свойствах треугольников и трапеций.

Первое, что нам нужно сделать - найти высоту треугольника ABC. Затем, с помощью найденной высоты мы сможем найти основание трапеции ADEC и, наконец, посчитать площадь треугольника ABC.

1. Найдем высоту треугольника ABC, обозначим ее через h:
Для этого воспользуемся свойством, что средняя линия треугольника параллельна и равна половине основания:
h = 2 * DE

2. Найдем основание трапеции ADEC, обозначим его через b:
Основание трапеции равно сумме оснований треугольника ABC и DE:
b = AB + 2 * DE

3. Теперь мы можем выразить площадь треугольника ABC через найденную высоту и основание:
Площадь треугольника равна половине произведения высоты на основание:
S = (1/2) * h * b

4. Подставим значения высоты и основания в формулу:
S = (1/2) * (2 * DE) * (AB + 2 * DE)
S = DE * (AB + 2 * DE)

5. У нас есть информация, что площадь трапеции ADEC равна 6, поэтому мы можем записать уравнение:
6 = DE * (AB + 2 * DE)

6. Решим это уравнение относительно одной переменной. Учитывая, что мы ищем площадь треугольника ABC, то AB - основание треугольника также неизвестно, поэтому оно остается в уравнении:
6 = DE * AB + 2 * DE^2

7. Теперь мы знаем, что площадь треугольника ABC равна 6, поэтому мы можем записать окончательное уравнение:
6 = DE * AB + 2 * DE^2

Таким образом, для решения задачи необходимо решить это квадратное уравнение относительно двух переменных DE и AB.