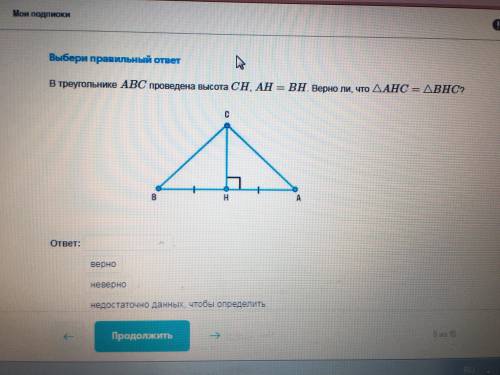
В треугольнике abc проведена высота ch,ah=bh.Верно ли,что треугольник ahc=bhc?

ответ:да

Пошаговое объяснение:

Если ah=ab то а=b

Чтобы ответить на данный вопрос, давайте рассмотрим данные сведения и используем основные свойства треугольников.

У нас есть треугольник ABC, в котором проведена высота CH (AH = BH). Нам нужно определить, верно ли, что треугольник AHC равен треугольнику BHC.

Для начала, давайте разберемся, что означает "треугольник AHC равен треугольнику BHC". Если два треугольника равны, это означает, что у них все стороны и углы равны.

1. Сравнение сторон:
Мы знаем, что AH = BH (так как AH = BH по условию).

2. Сравнение углов:
Угол AHC и угол BHC находятся при соответствующих сторонах AH и BH (так как построены из одной точки и до одной прямой).

Теперь давайте рассмотрим все условия, чтобы понять, верно ли утверждение или нет:

1. Стороны AH и BH равны, поэтому сторона AH = стороне BH.
2. Углы AHC и BHC равны по условию, так как они соответствующие углы при равных сторонах.

Таким образом, у нас есть две равные стороны и один равный угол в треугольнике AHC и BHC.

Из этого мы можем сделать вывод, что треугольник AHC равен треугольнику BHC (по критерию равенства двух треугольников, имеющих две равные стороны и один равный угол).

Так что ответ на данный вопрос: ДА, треугольник AHC равен треугольнику BHC.

Я надеюсь, что я смог просто и понятно объяснить ответ на этот вопрос! Если у тебя есть еще вопросы, не стесняйся задавать!