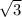В треугольнике ABC биссектрисы углов BAC и BCA пересекают высоту BH в точках P и Q соответственно (точка H лежит на стороне AC, точка P лежит между точками H и Q).Найдите площадь S треугольника ABC, если BQ = 14, QP=4, PH =9.
Другие вопросы по теме Математика
Популярные вопросы
- составить 5 вопросов на тему интернет по языку с переводом на ))...
3 - Как от большего смешанного отнять меньшее смешанное...
2 - Может ли кассовый работник держать на рабочем месте сумку с личными...
3 - Na2so4 + cucl2=2nacl+cuso4 реакция ионного обмена...
1 - Чим зумовлюється надзвичайна різноманітність білків? / чем объясняется...
1 - Велосипед ехал t ч со скоростью 10км/ч. постройте график движения...
2 - Всякий, кто вместо одного колоса или одного стебля травы сумеете...
3 - Сравни соленость воды на таллиннском и рижском побережьях. в чем...
1 - кто автор белый бим чёрное ухо,стрекоза и муравей,море,пудель арто,казетта....
3 - Какое важное для россии событие произошло в 1721 году...
3
Через св-во биссектрисы:
PH:BP=AH:AB=9:18=1:2
Пусть AH=x, тогда AB=2x
Через Пифагора: 3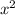 =
=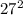
x=9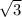
Аналогично, CH:BC=QH:BQ=13:14
Пусть CH=y, тогда BC=14:13y
Пифагор: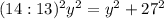
Переносим игрек влево и через разность квадратов: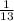 *
*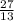
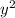 =
=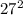
Делим обе части на 27 и получаем: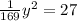
Это основание. А площадь - это половина высоты на основание:
S=0.5*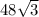 *27=648
*27=648