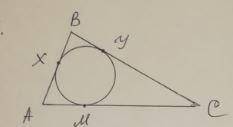
В треугольник АВС вписана окружность. Х, У, М-точки касания окружности со сторонами АВ, ВС, АС соответственно. Найдите длину ВХ, если АМ=7см, МС=11см, а периметр треугольника АВС равен 44см

Добрый день! Давайте разберем эту задачу.

У нас есть вписанный треугольник АВС, в котором Х, У и М - точки касания окружности со сторонами АВ, ВС и АС соответственно. Нам нужно найти длину отрезка ВХ.

Давайте воспользуемся свойством вписанного треугольника.

Свойство 1: В треугольнике, вписанном в окружность, прямые, проведенные из вершин к точкам касания со сторонами, являются высотами треугольника.

Это значит, что отрезки АМ, МС и БМ - высоты треугольника АВС.

Теперь нам нужно использовать свойство прямоугольного треугольника.

Свойство 2: В прямоугольном треугольнике, высота, проведенная из прямого угла к гипотенузе, делит треугольник на два подобных треугольника, и отношение длины отрезка гипотенузы, лежащего между вершиной и основанием, к длине всей гипотенузы равно отношению длины части гипотенузы, лежащей между основанием и точкой пересечения высоты, к длине основания.

Применим это свойство к нашей задаче.

Мы видим, что отрезок МС является основанием прямоугольного треугольника ВМС, а АМ является высотой, проведенной из прямого угла треугольника ВМС. Вершина В будет являться вершиной прямого угла.

Теперь воспользуемся данной величиной:

ВМ / МС = АМ / ВС

Заменим значения: ВМ / 11 = 7 / 20

Теперь найдем ВМ:

ВМ = (7 / 20) * 11

Умножим и получим ВМ = 77 / 20

Теперь, чтобы найти длину отрезка ВХ, нам нужно вычесть отрезок ВМ из длины стороны АВ:

ВХ = АВ - ВМ

Значение стороны АВ мы не знаем. Но мы знаем, что периметр треугольника АВС равен 44 см. Периметр треугольника равен сумме длин всех его сторон. Поэтому:

Периметр = АВ + ВС + АС

44 = АВ + ВС + АС

Мы знаем, что отрезок АМ равен 7 см, отрезок МС равен 11 см, значит, сторона АВ равна (АМ + МС). Подставим значения:

44 = (АМ + МС) + ВС + АС

44 = (7 + 11) + ВС + АС

44 = 18 + ВС + АС

Так как мы не знаем значения ВС и АС, они оба равны А. Поэтому:

44 = 18 + 2А

Теперь найдем значение А:

44 - 18 = 2А

26 = 2А

А = 26 / 2

А = 13

Теперь мы знаем значение стороны АВ, и можем найти длину отрезка ВХ:

ВХ = АВ - ВМ

ВХ = 13 - (77 / 20)

Теперь найдем значение:

ВХ = 260 / 20 - 77 / 20

ВХ = (260 - 77) / 20

ВХ = 183 / 20

ВХ = 9.15 см

Таким образом, длина отрезка ВХ составляет 9.15 см.

Надеюсь, это решение было понятным и подробным. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задать их. Я всегда готов помочь!