В ТЕТРАЭДЕ АBCD ТОЧКИ M, P, СООТВЕТСТВЕННО СЕРЕДИНЫ РЁБЕР AD, CD, BD УКАЖИТК ВЕРНЫЕ УТВЕРЖДЕНИЯ А) ПРЯМАЯ МК ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ АВС
Б) ПРЯМЫЕ МD И ВС СКРЕЩИВАЮЩИЕСЯ
В) ПЛОСКОСТЬ MPK ПАРАЛЛЕЛЬНА ПЛОСКОСТИ BCD
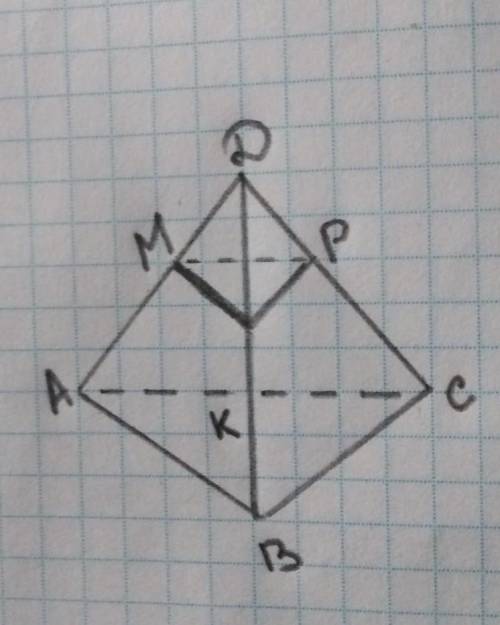
Другие вопросы по теме Математика
Популярные вопросы
- Нужно полное решение. Во легкий, надо проверить ответ, не ставьте...
3 - Передайте следующие предложения в страдательный залог: I haven t...
1 - Выпишите все верные утверждения...
3 - Яке значення воло- сяного покриву у житті ссавців?...
3 - Центр кола,описаного навколо трикутника,збігається із серединою сторони...
2 - Благодарность за что? За конфеты. Падеж какой?...
1 - Для расширения предела измерения амперметра в 50 раз подключается...
3 - Робот-пылесос Robo очищает за час в 4 раза большуюплощадь, чем Clean....
3 - Рус. В качестве сырья для получения етину используют кальций карбид....
3 - Какие современные артистывы знаете в лебедином озере?...
2
А) ПРЯМАЯ МК ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ АВС - верно.
Признак параллельности прямой и плоскости: Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости. Рассмотрим треугольник АВД. М и К середины сторон, значит МК - средняя линяя. Средняя линия треугольника параллельна основанию, т.е. МК||АВ. АВ лежит в плоскости АВС. Отсюда следует, что МК|| (АВС)
Б) ПРЯМЫЕ МD И ВС СКРЕЩИВАЮЩИЕСЯ - верно
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся. Рассмотрим плоскость АВС. ВС лежит в этой плоскости. МД пересекает эту плоскость в точке А, не принадлежащей ВС. Значит МД и ВС скрещиваются.
В) ПЛОСКОСТЬ MPK ПАРАЛЛЕЛЬНА ПЛОСКОСТИ BCD - неверно
Две плоскости называются параллельными, если они не имеют общих точек.
Плоскости МКР и ВСД пересекаются по прямой КР, значит они не могут быть параллельны
ответ: АБ