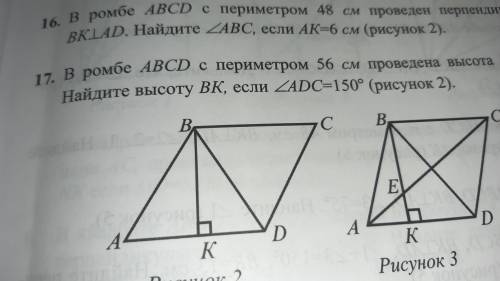
В ромбе ABCD с острым углом 60° проведён перпендикуляр BK AD Найдите диагональ BD если AK равен 7 см

Для решения данной задачи нам потребуется использовать свойства ромба.

Дано:
В ромбе ABCD угол B равен 60°.
Длина отрезка AK равна 7 см.

Необходимо найти:
Длину диагонали BD.

Решение:

1. По свойству ромба, диагонали ромба перпендикулярны между собой. Поэтому отрезок BK будет являться высотой ромба.

2. Для нахождения длины диагонали BD воспользуемся теоремой Пифагора в треугольнике ABD.

3. Зная, что BAK является прямым углом (так как BK перпендикулярен AD), мы можем найти длину отрезка AB по теореме Пифагора: AB² = AK² + BK².

4. Так как AK равен 7 см, а угол B равен 60°, мы можем найти длину отрезка BK с помощью тригонометрических соотношений. Для этого воспользуемся соотношением тангенса угла B: tan(B) = BK / AK.

5. Подставим известные значения: tan(60°) = BK / 7 см. Раскрывая тангенс 60°, мы получим корень из 3 (так же известный как √3).

6. Теперь мы можем найти значение BK. Рассмотрим полученное уравнение: √3 = BK / 7.
Перемножим обе части уравнения на 7, чтобы избавиться от знаменателя: √3 * 7 = BK.
Упрощаем выражение: BK = 7√3.

7. Теперь, имея длину BK, мы можем найти длину AB:
AB² = AK² + BK².
Подставляем известные значения: AB² = 7² + (7√3)².
Раскрываем скобки: AB² = 49 + 49 * 3.
Упрощаем выражение: AB² = 49 + 147.
AB² = 196.

8. Найдем квадратный корень из AB², чтобы найти длину AB: AB = √196 = 14 см.

9. Так как нам нужно найти длину диагонали BD, и диагонали ромба равны между собой, то BD = AB = 14 см.

Ответ: Длина диагонали BD равна 14 см.