В разложении (x+y)^6 найти коэффициент при x^2, y^4
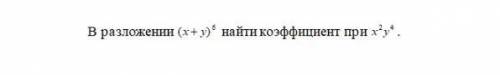
Другие вопросы по теме Математика
Популярные вопросы
- Таблица Внешняя политика консульства и империи во Франции...
2 - Что заставило Наполеона подписать акт отречения от престола?...
3 - Условия свободного капитализма...
1 - Какие идеи эпохи Просвещения стали чертами либерализма?...
1 - Сравнительная таблица основные социальные учения XIX в. (Либерализм, Консерватизм,...
3 - Почему человек должен быть свободным?...
2 - Назовите известных вам социалистов-утопистов XIX в....
1 - В каком программном документе были изложены основные принципы марксистского...
2 - Составьте план развернутого ответа по теме «Эпоха свободного капитализма»,...
2 - Какая из английских партий приняла идеи консерватизма в качестве своей идеологии?...
2
Пошаговое объяснение:
(y+x)^6=((x+y)^2)^3=(x²+2xy+y²)^3 получаешь x⁶+6x⁵y+15x⁴y²+20x³y³+15x²y⁴+ 6xy⁵+y⁶
15 Кофф.
В нашем случае, n = 6, a = x, b = y. Мы хотим найти коэффициент при x^2, y^4, поэтому у нас должно быть x^2 и y^4 в разложении.
Давайте обратимся к формуле Бинома Ньютона и найдем нужный коэффициент.
C(6, 4)x^2 y^4 = C(6, 4) * x^2 * y^4
Теперь нам нужно найти биномиальный коэффициент C(6, 4). Биномиальный коэффициент C(n, k) вычисляется как C(n, k) = n! / (k! * (n - k)!), где n! - факториал числа n.
C(6, 4) = 6! / (4! * (6 - 4)!)
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720
4! = 4 * 3 * 2 * 1 = 24
(6 - 4)! = 2! = 2 * 1 = 2
Теперь посчитаем:
C(6, 4) = 720 / (24 * 2) = 720 / 48 = 15
Подставим это значение обратно в формулу:
C(6, 4)x^2 y^4 = 15 * x^2 * y^4
Таким образом, коэффициент при x^2, y^4 в разложении (x+y)^6 равен 15.