1. Математика
  2. в равнобедренный треугольник

в равнобедренный треугольник с основанием 18 вписана окружность радиуса 3. Найдите периметр треугольника. Варианты ответов -фото


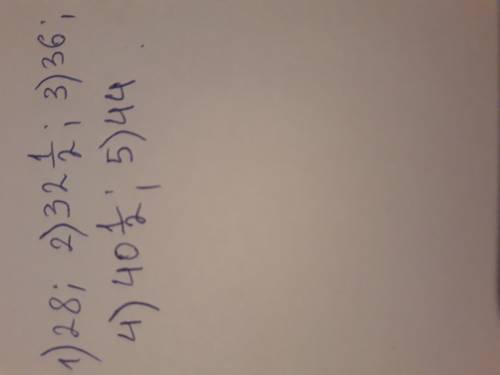
в равнобедренный треугольник с основанием 18 вписана окружность радиуса 3. Найдите периметр треуголь

12unicorn12 12unicorn12    2   11.08.2020 16:50    0

Ответы
OVSANKASIR OVSANKASIR  15.10.2020 15:51

4)40 \frac{1}{2} = 40.5

Пошаговое объяснение:

обозначим вершины треугольника А В С с основанием АС и боковыми сторонами АВ и ВС. Если ∆АВС- равнобедренный то АВ=ВС. Пусть АВ=ВС=х и составим уравнение используя сокращённую формулу для поиска радиуса вписанной окружности:

r = \frac{ac}{2} × \frac{ \sqrt{2x - ac} }{ \sqrt{2x + ac} }

подставим известные нам значения в это уравнение:

3 = \frac{18}{2} \times \sqrt{ \frac{2x - 18}{2x + 18} }

3 = 9 \sqrt{ \frac{2x - 18}{2x + 18} }

возведём обе части уравнения в квадрат:

9 = 81 \times \frac{2x - 18}{2x + 18}

9 = 81 \times \frac{2(x - 9)}{2(x + 9)}

9 = 81 \times \frac{x - 9}{x + 9}

поменяем местами левую и правую часть уравнения:

81 \times \frac{x - 9}{x + 9} = 9

\frac{x - 9}{x + 9} = \frac{9}{81}

\frac{x - 9}{x + 9} = \frac{1}{9}

перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:

9(х–9)=х+9

9х–81–х=9

8х=9+81

8х=90

х=90÷8=11,25

Итак: АВ=ВС=11,25

И теперь найдём периметр треугольника зная все его стороны: Р=2×11,25+18=40,5


в равнобедренный треугольник с основанием 18 вписана окружность радиуса 3. Найдите периметр треуголь
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
dsassaraf dsassaraf  18.05.2019 10:30
Пчелы собирают нектар с клеверного поля-1200м от пасеки и с луга-в 600м от пасеки.от поля до пасеки пчела летит на 2мин дольше, чем от луга до пасеки.сколько времени тратит пчела...
yliatroshenko yliatroshenko  18.05.2019 10:30
Автомобіль проїхав480км за 6год.за скільки годин подолає цю відстань мотоцикл якщо його швидкість становить3/4 швидкості автомобіля...
AzamatAmangaliev1 AzamatAmangaliev1  18.05.2019 10:30
36400: 700= подскажите как в столбик решить этот пример...
AlinaRai AlinaRai  18.05.2019 10:30
Шмель и оса полетели с поля в одном направление. зная, что шмель летел со скоростью 50м/мин, а оса 150м/мин,ответь на каком растоянии от поля оса догонит шмеля, если он вылетел с...
анна2255 анна2255  18.05.2019 10:30
Учитель задал . в результате количество решивших её мальчиков оказалось равным количеству не решивших девочек. кого в классе больше - решивших или (решение, объяснение) заранее !...
muraitovaayana2 muraitovaayana2  18.05.2019 10:30
Охарактеризовать героев из сказки и. губарёва королевство кривых зеркал гурда, оли и яло...
dhvcn dhvcn  18.05.2019 10:30
Чем занимаются жители украины в наши дни...
fdglksjf fdglksjf  18.05.2019 10:30
Товар стоил 150 руб. его цена повысилась на 12% сколько теперь стоит этот товар? не только решите но и объясните почему )...
Sniper009902 Sniper009902  18.05.2019 10:30
Влотерее из 40 билетов 8 выигрышных.какова вероятность того,что среди первых пяти наугад выбранных билетов два будут выигрышными?...
ВладаФролова01 ВладаФролова01  18.05.2019 10:30
Решить . уже задавала эту , но в раз забыла плюс поставить, теперь все на месте) ( c1, егэ) (4sinx-2cos2x-1)/(cos2x+sqrt3cosx-2)=0...

Популярные вопросы