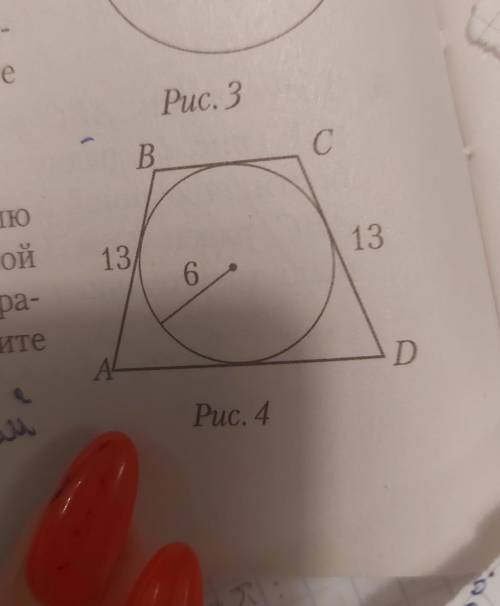
в равнобедренную трапецию с боковой стороной равной 13 см вписана окружность с радиусом 6 см найдите площадь трапеции​

Чтобы найти площадь равнобедренной трапеции, в которую вписана окружность, нам понадобится использовать теорему Пифагора и формулу площади окружности.

Дано:
- Боковая сторона равна 13 см
- Радиус вписанной окружности равен 6 см

Первым шагом нам нужно найти высоту трапеции. Высота трапеции - это отрезок, опущенный из вершины трапеции на основание. Заметим, что этот отрезок является радиусом окружности, вписанной в трапецию.

Так как у нас равнобедренная трапеция, мы знаем, что основания равны. Обозначим это расстояние как b см (базовая сторона).

По теореме Пифагора, для равнобедренной трапеции высота h связана с основанием b и боковой стороной а следующим образом:

h^2 = a^2 - (1/4)(b^2)

Теперь мы можем выразить высоту h через известные значения:

h^2 = 6^2 - (1/4)(13^2)
h^2 = 36 - (1/4)(169)
h^2 = 36 - 42.25
h^2 = -6.25

Мы получили отрицательное значение для h^2, что говорит о том, что такая трапеция не существует. Вероятно, в задаче была допущена ошибка или неправильно указаны данные.