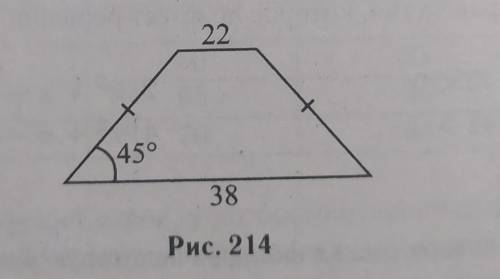
В равнобедренной трапеции основания равны 22 и 38, а один из углов между боковой стороной и основанием равен 45° (см. рис. 214). Найдите
Площадь трапеции.​

Для решения этой задачи нам понадобятся знания о формулах для площади трапеции и свойствах равнобедренных треугольников. Давайте сначала разберем, как получить площадь трапеции.

Площадь трапеции можно найти, используя формулу:

S = (a + b) * h / 2,

где a и b - длины оснований, а h - высота трапеции.

В данной задаче нам даны длины оснований. Однако, нам не дана высота трапеции.

Чтобы найти высоту, мы можем воспользоваться свойствами равнобедренных треугольников. В равнобедренном треугольнике две стороны равны (основания трапеции), и угол между ними (45° в данном случае) также равен.

Таким образом, мы можем разделить равнобедренную трапецию на два прямоугольных треугольника со сторонами a/2, b/2 и углом 45° между горизонтальным основанием и боковой стороной.

Для нахождения высоты h, мы можем применить тригонометрический закон синусов в одном из этих треугольников:

sin(45°) = h / (a/2).

Упростим это выражение:

h = (a/2) * sin(45°).

Теперь мы можем подставить значения a и b в формулу для нахождения площади трапеции:

S = (a + b) * h / 2.

Вот пошаговое решение:

1. Рассчитаем высоту h, используя формулу h = (a/2) * sin(45°). Подставим значения для a и угла:

h = (22/2) * sin(45°),
h = 11 * 0.7071,
h ≈ 7.778.

2. Подставим значения a, b и h в формулу для площади трапеции:

S = (22 + 38) * 7.778 / 2,
S = 60 * 7.778 / 2,
S ≈ 233.34.

Таким образом, площадь равнобедренной трапеции равна около 233.34 квадратных единиц.