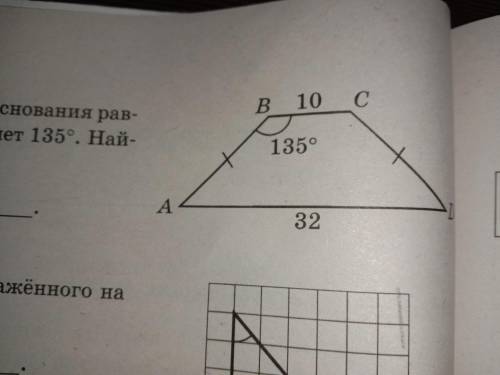
В равнобедренной трапеции ABCD основания равны 10 и 32, а один из углов составляет 135°. Найдите площадь трапеции.

Добрый день, ученик! Давайте решим эту задачу вместе.

У нас есть равнобедренная трапеция ABCD, в которой основания равны 10 и 32 единицам, а один из углов составляет 135°. Нам нужно найти площадь этой трапеции.

Для начала, давайте обратим внимание на то, что в равнобедренной трапеции, боковые стороны равны. Поэтому, если мы найдем эту боковую сторону, то сможем найти площадь.

Для этого, давайте разделим трапецию на два прямоугольных треугольника, используя высоту трапеции. Поскольку один из углов составляет 135°, то заметим, что другой угол тоже будет равным 135°, так как сумма углов треугольника равна 180°.

В каждом треугольнике у нас есть две стороны и угол между ними. Мы знаем, что одна сторона равна 10 единицам, а знаем лишь незначительную информацию о двух углах.

Используя тригонометрию, мы можем вычислить вторую сторону треугольника. Для этого давайте воспользуемся формулой косинусов, которая выглядит так:

c^2 = a^2 + b^2 - 2*a*b*cos(C)

Где c - сторона напротив угла C, a и b - две другие стороны.

В нашем случае, если мы применим формулу косинусов ко второму треугольнику, получим следующее:

b^2 = 10^2 + 10^2 - 2*10*10*cos(135°)

Теперь давайте вычислим это:

b^2 = 100 + 100 - 2*10*10*cos(135°)

b^2 = 200 - 200*cos(135°)

Теперь, давайте найдем косинус угла 135°:

cos(135°) = cos(45° + 90°) = - cos(45°) = -√2/2

Подставим это обратно в формулу:

b^2 = 200 - 200*(-√2/2)

b^2 = 200 + 200√2/2

b^2 = 200 + 100√2

b^2 = 300 + 100√2

b ≈ √(300 + 100√2)

Теперь у нас есть значение боковой стороны. Давайте продолжим решение.

Чтобы найти площадь трапеции, мы можем использовать формулу:

Площадь = (сумма оснований * высота) / 2

В нашем случае, сумма оснований равна 10 + 32 = 42. Изначально нам не дана высота трапеции, но мы знаем, что треугольники, образованные основаниями и высотой, являются прямоугольными треугольниками.

Таким образом, мы можем использовать теорему Пифагора для нахождения высоты треугольника. Формула теоремы Пифагора:

a^2 + b^2 = c^2

Где a и b - катеты прямоугольного треугольника, а c - гипотенуза.

В нашем случае, у нас есть половина основания (5 и 16 единиц) и длина боковой стороны треугольника после вычислений (√(300 + 100√2) единиц). Подставим это в формулу:

(5^2 + h^2) + (16^2 + h^2) = (√(300 + 100√2))^2

25 + h^2 + 256 + h^2 = 300 + 100√2

2h^2 + 281 = 300 + 100√2

2h^2 = 100√2 - 219

h^2 = (100√2 - 219) / 2

h ≈ √((100√2 - 219) / 2)

Теперь у нас есть значение высоты. Мы можем подставить значения в формулу для нахождения площади трапеции:

Площадь = (42 * √((100√2 - 219) / 2)) / 2

После всех вычислений мы получим площадь трапеции.