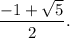в прямоугольном треугольнике АВС с прамым углом С проведены бис. AL и высотa CH. Найдите косинус угла ВАС, если НL//AC
Другие вопросы по теме Математика
Популярные вопросы
- Спортсменов построили в колонну по 6 человек в ряду, а затем перестроили,...
2 - Число разложили на простые множители и получили такое произведение:...
2 - Найдите первое трёхзначное число, являющееся простым. б) Определите,...
1 - Задуманное число больше 30, но меньше 50; его называют, когда...
3 - Какое утверждение верно? 1) Все простые числа — нечётные. 2) Все...
3 - Составьте все возможные трёхзначные числа из цифр 1, 2 и 7 (без...
1 - Может ли сумма двух простых чисел быть простым числом? б) Может...
3 - Назовите все двузначные числа, меньшие 30, разложение на простые...
1 - Как известно, простое число имеет два делителя. А сколько делителей...
1 - Простые числа, разность которых равна 2, называют числами-близнецами....
1
Пусть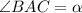 , тогда
, тогда 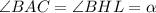 как соответственные.
как соответственные.
Высота, проведенная из вершины прямого угла, есть среднее геометрическое между проекциями катетов:
По свойству биссектрисы :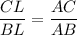 . Тогда
. Тогда
Воспользуемся следующими тригонометрическими свойствами
Последнее уравнение решается как квадратное уравнение относительно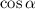 .
.
Значение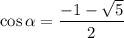 — постороннее, поскольку косинус принимает значения от -1 до 1.
— постороннее, поскольку косинус принимает значения от -1 до 1.
ответ: