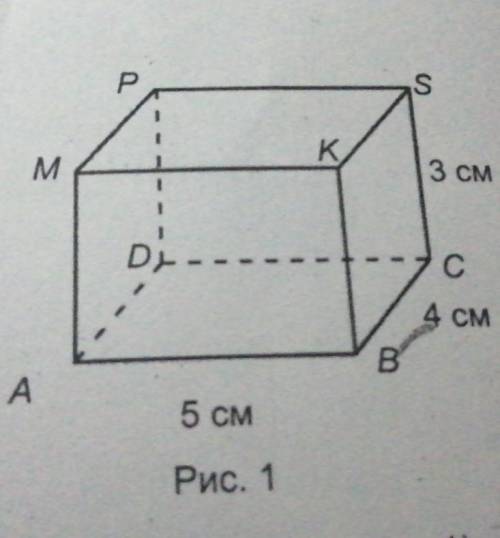
В прямоугольном параллелепипеде ABCDMKSP равны ребра (смотри рисунок 1).
P
к
M
3 см
1) SC и AD
2) DC и MP
3) АВи KS
4) SC и AM
Рис. 1​

1) SC и AD: На рисунке видно, что SC и AD - это две боковые грани параллелепипеда. Так как все ребра параллелепипеда равны, то ребра SC и AD также равны. 2) DC и MP: DC - это одно из ребер основания параллелепипеда, а MP - это диагональ грани параллелепипеда. Обратимся к прямоугольному треугольнику DMP внутри параллелепипеда. У него сторона MP равна основанию DC параллелограмма, а сторона DP равна высоте DC параллелограмма. Так как параллелепипед является прямоугольным, значит угол D у треугольника DMP прямой. А по теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Применим эту теорему к треугольнику DMP: DM^2 = MP^2 + DP^2 Так как ребра параллелепипеда равны, то DM = DC и DP = SC. Подставим это в уравнение: DC^2 = MP^2 + SC^2 То есть ребра DC и MP не являются равными. 3) AB и KS: AB - это одно из ребер основания параллелепипеда, а KS - это диагональ грани параллелепипеда. Аналогично предыдущему пункту, рассмотрим прямоугольный треугольник ABS. У него AB - это основание, а BS - это диагональ грани параллелепипеда. Также, так как треугольник ABS является прямоугольным, применим теорему Пифагора: AS^2 = BS^2 + AB^2 Так как ребра параллелепипеда равны, то AB = KS. Подставим это в уравнение: AS^2 = BS^2 + KS^2 То есть ребра AB и KS равны. 4) SC и AM: SC - это одно из ребер боковой грани параллелепипеда, а AM - это диагональ параллелепипеда. Аналогично предыдущим пунктам, рассмотрим прямоугольный треугольник AMC. У него AM - это диагональ параллелепипеда, а AC - это ребро боковой грани параллелепипеда. Также, так как треугольник AMC является прямоугольным, применим теорему Пифагора: AM^2 = AC^2 + MC^2 Так как ребра параллелепипеда равны, то AC = SC, MC = SM. Подставим это в уравнение: AM^2 = SC^2 + SM^2 То есть ребра SC и AM не являются равными. Для лучшего понимания ответа, мы рассмотрели прямоугольные треугольники, вокруг которых происходят рассуждения. Теорема Пифагора, которую мы использовали в решении, основана на свойствах прямоугольных треугольников и гласит, что квадрат гипотенузы равен сумме квадратов катетов.