В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины ребер: АВ = √3, АD = √6 и АА1 = √5. Найдите угол между прямыми A1B и AC1.

Ответы

hfdgddcju 12.07.2022 12:19

Поместим прямоугольный параллелепипед в систему координат так, чтобы вершина А совпала с началом координат, ребра AB, AD и AA₁ лежали на координатных осях.

Таким образом,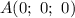 $A(0;\ 0;\ 0)$ .

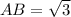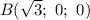Так как $AB=\sqrt{3}$ , то $B(\sqrt{3} ;\ 0;\ 0)$ .

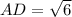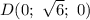Так как $AD=\sqrt{6}$ , то $D(0;\ \sqrt{6};\ 0)$ .

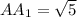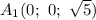Так как $AA_1=\sqrt{5}$ , то $A_1(0 ;\ 0;\ \sqrt{5})$ .

Исходя из чертежа, вершина С₁ имеет абсциссу, равную абсциссе вершины В, ординату, равную ординате вершины D, и аппликату, р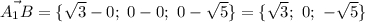 $\vec{A_1B}=\{\sqrt{3} -0;\ 0-0;\ 0-\sqrt{5} \}=\{\sqrt{3} ;\ 0;\ -\sqrt{5} \}$

$\vec{AC_1}=\{\sqrt{3} -0;\ \sqrt{6} -0;\ \sqrt{5}-0 \}=\{\sqrt{3} ;\ \sqrt{6} ;\ \sqrt{5} \}$

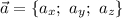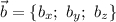Для нахождения угла между прямыми, определяемыми направляющими векторами $\vec{a}=\{a_x;\ a_y;\ a_z\}$ и $\vec{b}=\{b_x;\ b_y;\ b_z\}$ , используется формула:

$\cos \varphi =\dfrac{|a_xb_x+a_yb_y+a_zb_z|}{\sqrt{a_x^2+a_y^2+a_z^2}\cdot \sqrt{b_x^2+b_y^2+b_z^2}}$

Получим:

$\cos \varphi =\dfrac{|\sqrt{3} \cdot\sqrt{3} +0\cdot\sqrt{6} -\sqrt{5}\cdot\sqrt{5} | }{\sqrt{(\sqrt{3})^2+0^2+(-\sqrt{5})^2}\cdot \sqrt{(\sqrt{3})^2+(\sqrt{6})^2+(\sqrt{5})^2}}=$

$=\dfrac{|3 +0 -5 | }{\sqrt{3+0+5}\cdot \sqrt{3+6+5}}=\dfrac{|-2 | }{\sqrt{8}\cdot \sqrt{14}}=\dfrac{2 }{2\sqrt{2}\cdot\sqrt{2}\cdot \sqrt{7}}=\dfrac{1 }{ 2\sqrt{7}}$