В прямоугольном параллелепипеде ABCDA1B1C1D1; ∠ABD=30°; BB1=9см; AD=20см.
Вычисли объём.
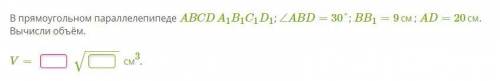
Другие вопросы по теме Математика
Популярные вопросы
- Вставь в предложения по смыслу слова.выдели орфограммы жи-ши ча-ща чу-щу птичьи...
2 - Составить диалог на тему день рождения почему то не получаетя...
1 - Состав летучего водородного соединения углерода...
1 - До яких явищ-фізичних чи хімічних-належить розчинення кристалічної речовини...
1 - Решить 167 400 : 27 - 91 * 62 в столбик...
2 - При каких значениях параметра а заданный многочлен имеет кратные корни (2x+5)(3x-1)(x-a)(x-2a)...
3 - Найдите множество целых значений х, при которых верно неравенство: а)-4 х 6...
3 - Вклассе поровну девочек и мальчиков. на 8 марта каждый мальчик подарил каждой...
1 - Как найти площадь квадрата вокруг которого описана окружность радиуса r...
1 - Можете написать все правила по языку! 5 класса...
3
1. Начнем с нахождения высоты параллелепипеда. Поскольку имеется прямоугольный треугольник ABD с углом в 30°, можно воспользоваться тригонометрическим соотношением. В данном случае нам известна длина стороны AB равная 9 см, и подвисающая сторона AD равна 20 см. Используем формулу тангенса:
танγ(∠ABD) = противолежащая/прилежащая = AD/AB
танγ(30°) = AD/AB
танγ(30°) = 20/9
Используя тригонометрическую таблицу или калькулятор, получаем, что тангенс 30° равен приблизительно 0,577.
0,577 = 20/9
Умножаем обе стороны уравнения на 9:
0,577 * 9 = 20
5,193 ≈ 20
Отсюда получаем, что высота AD равна 5,193 см.
2. Теперь, когда у нас есть высота AD, можно найти объем параллелепипеда. Для этого умножаем длину AB (т.е. сторону равностороннего треугольника BB1) на ширину BC1 (т.е. BC) и на высоту AD:
Объем параллелепипеда = AB * BC1 * AD
Объем параллелепипеда = 9 см * BC * 5,193 см
Вопрос не содержит данных о значении BC, так что его значение необходимо вычислить.
3. Около треугольника AB1C1 можно построить еще один равносторонний треугольник A1B1C, так как BB1 = 9 см. Значит, сторона BC равна 9 см.
Объем параллелепипеда = 9 см * 9 см * 5,193 см = 425,97 см³
Ответ: Объем параллелепипеда равен 425,97 см³.